General raycasting to avoid overdrawing

Testing if a wall is completely hidden

Note: for clarity the images in this articles shows walls aligned on a grid, but the algorithms described here works with walls of any direction,
and their end does not need to lie on grid boundaries.

Imagine a game where you are inside a maze with walls.
The algorithms I will describe works with a top-view 2D representation, but if we want to represent them in 3D, there are some important things we will assume:
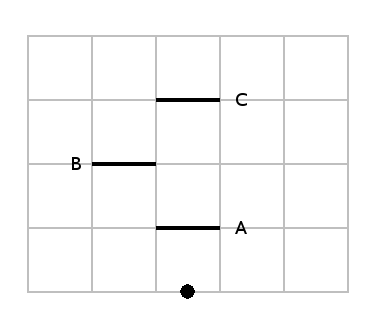
So a top-down view of our maze with a few walls can look like this, with the dot representing the "player":
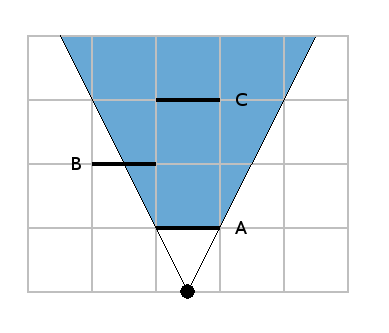
Can the player see every wall when, he looks toward the up ?
Let's see what the wall A hides from his point of view. Everything in blue in the following image is hidden:
The wall C is completly hidden and the wall B is only partly visible.
But can we write an algorithm to retrieve those informations ?
Let's try to cast rays starting at the player and going towards the ends of the wall C:
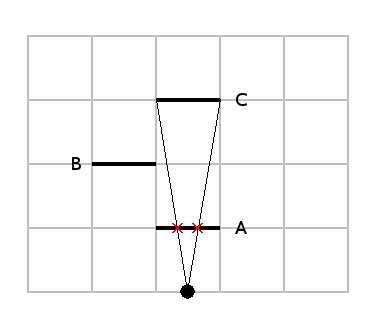
We can see that both rays intersects with wall A. Now let's try with wall B:
One of the ray intersects wall A and the other intersects nothing.
Obviously if we tried with wall A, the rays would not intersect anything because it is the nearest wall.
So here is the general algorithm:

	Initialise a variable "dist" with a big value, or infinity if the variable type allows it.
	Set up a ray that start from the player and that goes towards one end of the wall we want to test.
	For each wall except the one we are testing
		If the ray intersects this wall then
			If the distance between the player and the intersection is lesser than "dist" then
				Set "dist" to this distance, it is also wise to store the identifier of the wall we hit in another variable
				
	Repeat the above algorithm with the ray that goes towards the other end of the wall we are testing
	If both rays have hit something, that's to say if both "dist" variables are lesser than the big value at the start, then
		If both "dist" are smaller than the distance to wall we are testing then
			Our wall is completely hidden.

Some words about the intersection routine

I did not go into details about the intersection algorithm, as you can find many on the net. And you would probably want
to choose one that fits yous needs - i.e. you could want to use an optimised algorithm if your walls are aligned on a grid,
or you could choose to use a more general algorithm that could be reused in other places in your game engine.

But be careful, on the net you will find all kind of algorithms, for intersection between 2 infinite lines, between a line and a segment,
between a ray and a segment... every combination is possible.
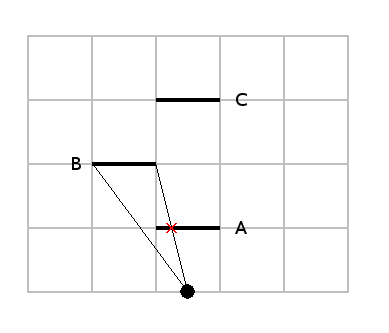
In our case we need that at least one of the two elements is a segment. Indeed, if you look at the diagram where we tested the wall B,
if we had seen the wall A as an inifinite line, the 2 rays would have intersected with it.

Pay also attention to the fact that some algorithms only tests if there is an intersection, and others really calculate it's position.
Finally, some algorithms will return you the distance of the intersection from a point, so you can avoid to calculate the distance to
the player afterwards.

Limitations of the algorithm

This algorithm works well in most of the cases when all the walls are about the same size, but if we use walls of very different size,
some cases will give strange results.
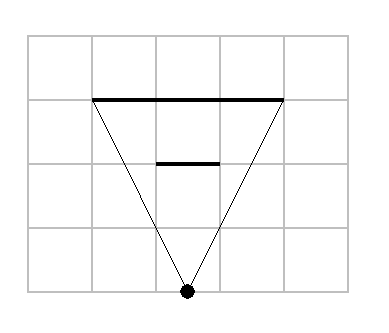
This case is not really a problem, as the algorithm didn't say that when there are no intersections the wall is completely visible.
In this case it is partially visible, but it add a constraint as we have to draw the farthest wall before the nearest one for this to work.
So we have to follow the painter's algorithm.
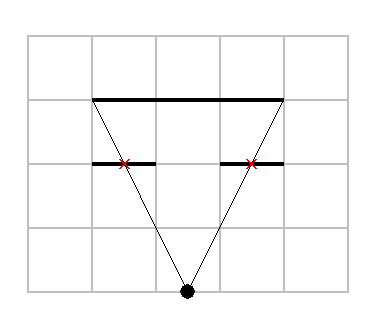
In this case the algorithm doesn't work at all. As both rays intersects, the large wall would be seen as hidden.
A workaround would be to cast more rays, or to split the wall into smaller ones, which is the same.
Well there isn't always an easy way to make an algorithm that works with all cases. This kind of problems often arise when you try to make a 3D software
that can handle walls or objects of very different sizes.
In most of the cases it is solved by asking a 3D artist to cut the wall into smaller chunks.
But we will see some ways to minimize those problems and to limit the overdrawing of hidden or partially hidden walls.

Handling partially hidden walls, towards ray-tracing

The above algorithm doesn't says us much about the partially hidden walls. We could resign ourselves to draw them completely, as at least a part of
them is visible, but let's see how the problem was handled in the firsts FPS like Wolfenstein or Doom.

Suppose we have to fill the screen completely one pixel at a time, we will naturally think about that in terms of lines:
We will start by filling the first line from the left to the right, then we will go downt to the second line, filling it from the left to the right...
Exactly the same way as we read a text in fact.

The first FPS reverted this way of thinking as they drew on the screen column after column.
Here you can see a screen where we begin to draw a wall. The pixel are magnified for a better understanding:
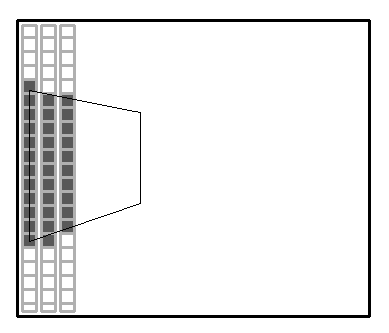
We start to draw the pixels of the walls on the first column, then the second column, and so on.
For each column we draw only one wall, so in the case of a partly visible wall, only the visible columns of it will be drawn.
Well, in fact in Doom, there could be more than one wall per column, as they put walls one above another to simulate different floors,
but that's another story...

So how does it works with our rays. To understand let's look at a top-down view:
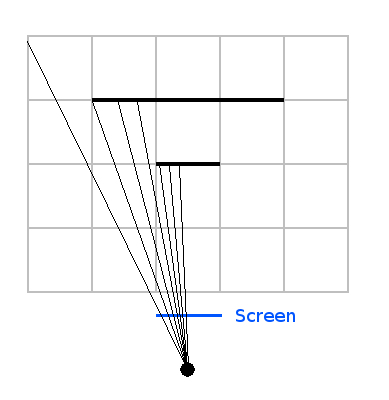
Imagine the player is holding the screen in front of him, at a given distance. In fact, this distance defines the width of the cone of vision.
For each column of the screen we cast a ray that starts at the player and that goes throught the screen's column - it takes only a little trigonometry
to find the equation of the ray.
Now if you look at the image you clearly see that the rays hits only the visible parts of the walls.

The algorithm for this is very similar to the one we saw before:

	For each column of the screen
	[
		Initialise a variable "dist" with a big value.
		Compute the equation of the ray.
		For each wall in the scene
		[
			If the ray intersects this wall then
				If the distance between the player and the intersection is lesser than "dist" then
					Set "dist" to this distance, it is also wise to store the identifier of the wall we hit in another variable
		]
		If "dist" is not equal to the big value, we hit a wall, then
			Draw the column of this wall
	]
The "dist" variable is used to calculate the height of the wall on the current column then a texture is applied on it.

Why did I talk about ray-tracing in the title?
Well, in this algorithm, we cast a ray for each column of the screen. The ray-tracing algorithm goes even farther as it casts a ray for every pixel
But then we have to take 3D rays, and this goes a little beyond the topic of this paper.

Optimisations

The speed of this algorithm depends how many walls we test in the loop. So imagine we are in a big maze with hundred of walls.
There a many optimisations we can do to limit the number of walls in the list before we apply the algorithm: But there is also an important way to speed-up the algorithm itself.
When we cast a ray from the player we only keep the nearest wall we hit. So if we could sort the walls according to their distance
to the player - from the nearest to the farthest, then when we apply then algorithm, at the first intersection we encounter we can
break out of the loop and avoid testing the following walls for this ray.

This sorting can be achieved easily with particular configurations, i.e. when walls lies on the boundaries of a grid.
But unfortunately it is much more difficult to find a algorithm which work in all the cases. Especially when the walls sizes can
vary greatly, you encounter problems like the ones we saw for the first algorithm.
That's why Doom used BSP trees.

Towards the perfect algorithm / Shadow-casting

Now I will explain briefly an algorithm that improves the first one we saw and that avoids the problems we encountered ,but you will see that
it is far more difficult to implement.

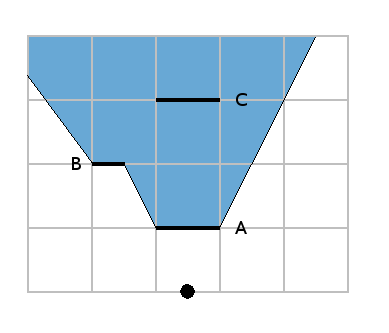
At the beginning of this article we began to draw the area that was hidden by wall A and we found that wall C lied completely inside of it.
If we erase the beginnings of the rays that comes from the player we get this:
Now we will do the same with the other walls and try to find the polygon that defines the bounds of the shadow area.
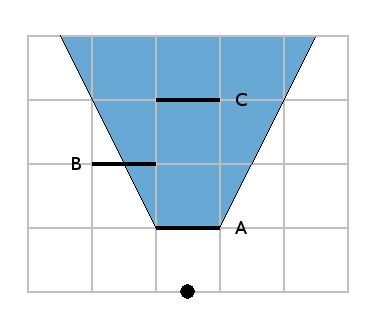
So let's draw the "cone of shadow" of wall B:
Again we will erase the beginnigs of the rays:
Now we will also erase the rays that lies inside the area. Note that we have to cut the ray coming from A:
We also cut wall B and erase the part that is inside the area:
Now, for the wall C, we cast the rays:
Then we erase the begginings of the rays:
Then we delete the rays that are inside the area:
Then, as we did for B, we erase the parts of the wall that lies inside the area.
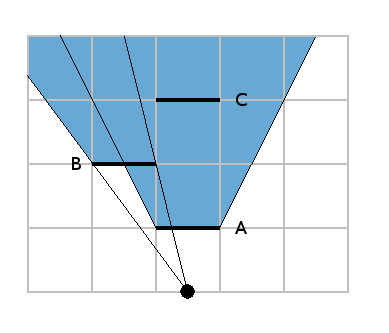
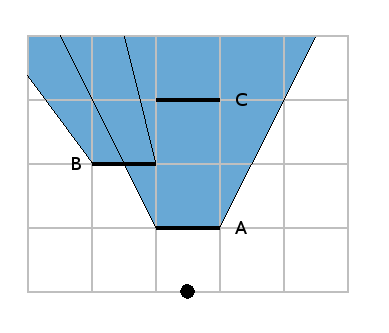
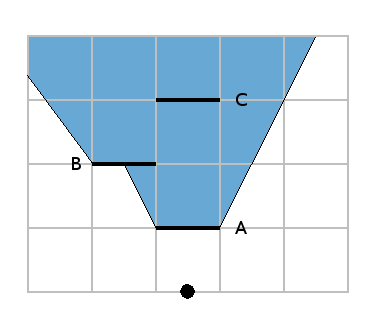
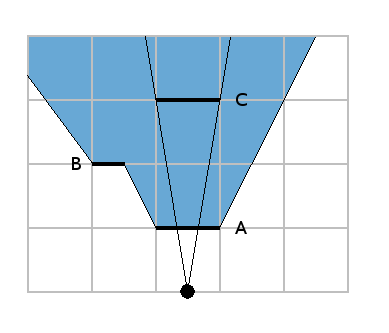
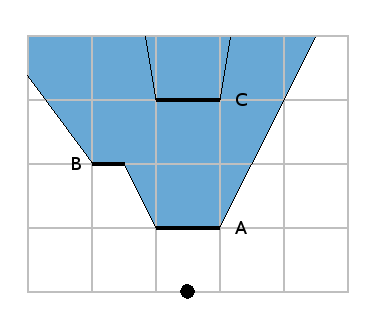
As the wall C is completely inside the area, we delete the whole wall:
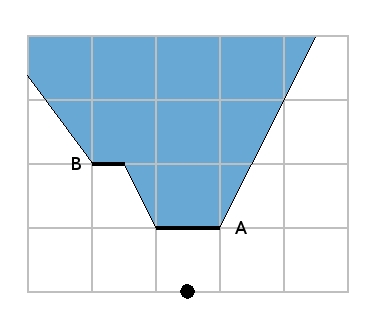
What we have left is the polygon we were looking for.
It is interesting to see that all the visible walls and walls parts lies on the edges of this polygon.

You can understand that, apart the way we would store the lines in memory, the hardest part of this algorithm
is when we cut the lines and erase the useless parts of them. It takes a bit of reflexion to handle all the cases
we can encounter.

For your interest a similar technique called "shadow volume" is used in 3D graphics to find how an object will cast
shadows on other objects or on the ground. But of course if you take an object with a shape more complex than a plain
wall, thing becomes a lot more difficult.