• Home
• 2D Geometry
• Contact

Vectors

This page displays mathematical formulas using a MathML script.
If you are reading this using Internet Explorer, I recommend you to accept the execution of this script when IE
asks it.

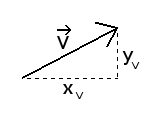
A vector is a geometric object that defines a length and a direction.
In geometry it is commonly represented with an arrow. But in programming we will represent it as its coordinates.
The aim of this article is to begin to write a vector class. And we we will add functions to this class in several
other articles.

Now imagine we have 2 points A and B.


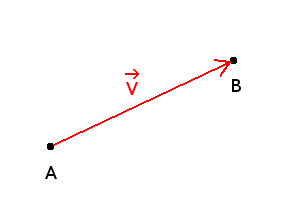
We can draw a vector $\overrightarrow{V}$ going from A to B.


Notice the little arrow over "V" it's a mathematical notation to say that it is a vector. Obviously in the code we
won't be able to add this graphical element.

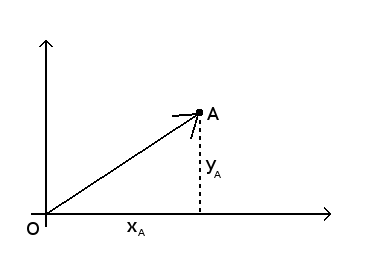
If the plane has a coordinates system, we can define the coordinates of the vector as the difference between the
coordinates of the destination point and the coordinates of the origin point.
That's to say that our vector's coordinates are (x_B-x_A, y_B-y_A).
But mathematicians often prefer to write them vertically $\left(\begin{array}{c}{x}_B-x_A\\ y_B-y_A\end{array}\right)$.

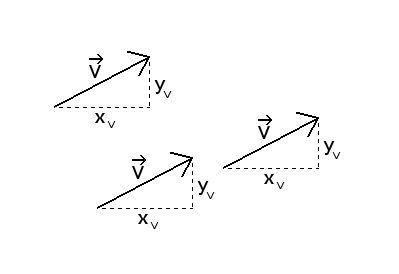
Now forget the points. The coordinates $\left(\begin{array}{c}{x}_V\\ y_V\end{array}\right)$ of the vector are only 2 numbers that represents its length and its
orientation.
This vector does not have to begin at point A. You can move it everywhere on the plane it will be the same vector
as long it has the same length and direction.


And that's where we start to write our vector class. It will simply hold the 2 coordinates of our vector.

		class Vec2f
		{
		public:
			Vec2f(const float _x = 0.0, const float _y = 0.0);

			float   x, y;
		};

		Vec2f::Vec2f(const float _x, const float _y)
		{
			x = _x;
			y = _y;
		}
				

I called it Vec2f because it has 2 coordinates. The "f" tells us these are floats.
Eventually we may later want to write a class with integer or double coordinates.

This class contains 2 coordinates, as the coordinates of a point.
So it could be useful if we could use it to store a point.
But would it make any sense ?
In fact the coordinates of a point can be seen as the coordinates of a vector going from the origin of the plane to
the point.


Remember we defined the coordinates of a vector as the difference of the coordinates of its end points.
In our case we have $\left(\begin{array}{c}{x}_A-x_O\\ y_A-y_O\end{array}\right)$.
As the coordinates of O are (0, 0), the coordinates of the point and the vector are the same.
This fact will help us a lot when we will talk about geometric transformations.

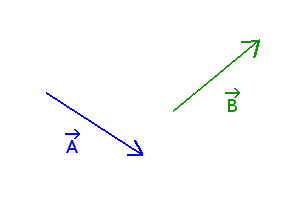
Suppose we have 2 vectors $\overrightarrow{A}\left(\begin{array}{c}{x}_A\\ y_A\end{array}\right)$ and $\overrightarrow{B}\left(\begin{array}{c}{x}_B\\ y_B\end{array}\right)$.


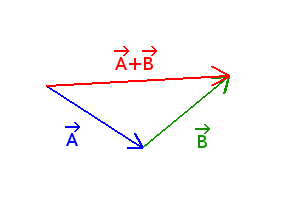
To get the coordinates of the sum vector, you simply add the coordinates of the 2 vectors.
So $\overrightarrow{A}+\overrightarrow{B}=\left(\begin{array}{c}{x}_A+x_B\\ y_A+y_B\end{array}\right)$.
Graphically you can see it as moving the vector $\overrightarrow{B}$ at the end of the vector $\overrightarrow{A}$.
The sum vector can be drawn starting at the origin of $\overrightarrow{A}$ and ending at the end of $\overrightarrow{B}$.

Now we can add the addition to our class by overloading the addition operator.

		Vec2f Vec2f::operator+(const Vec2f& a)
		{
			Vec2f   result;

			result.x = x + a.x;
			result.y = y + a.y;

			return result;
		}
				

And we can write the += operator too.

		Vec2f& Vec2f::operator+=(const Vec2f& a)
		{
			x += a.x;
			y += a.y;
			return *this;
		}
				

This way we can add vectors as we would do with simple numbers. In example:

		Vec2f	v1(1.0, 2.0);
		Vec2f	v2(3.0, 4.0);
		Vec2f	v3;
		
		v3 = v1 + v2;
				

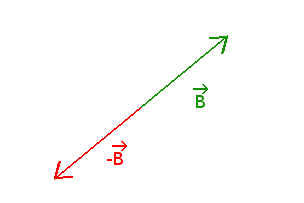
The opposite of a vector is the vector which coordinates are the opposite of the original vector.
Graphically it looks like the original vector but it goes in the other direction.


We will define that with the unary minus operator.

		Vec2f Vec2f::operator-()
		{
			Vec2f   result;

			result.x = -x;
			result.y = -y;

			return result;
		}
				

We can use it like this:

		v2 = -v1;
				

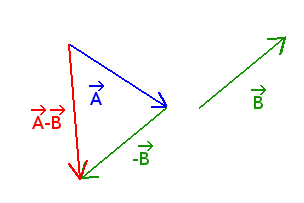
Substracting the vector $\overrightarrow{B}$ from the vector $\overrightarrow{A}$ is the same as adding its opposite.


We can now define the binary minus and the -= operators.

		Vec2f Vec2f::operator-(const Vec2f& a)
		{
			Vec2f   result;

			result.x = x - a.x;
			result.y = y - a.y;

			return result;
		}

		Vec2f& Vec2f::operator-=(const Vec2f& a)
		{
			x -= a.x;
			y -= a.y;
			return *this;
		}
				

The magnitude of a vector is its length - sometimes it can also be called its "norm".
With this vector:


By applying the Pythagoras' theorem, we have:
${\Vert \overrightarrow{V}\Vert }^2={x_V}^2+{y_V}^2$
And by taking the square root:
$\Vert \overrightarrow{V}\Vert =\sqrt{{x_V}^2+{y_V}^2}$
We will add the 2 formulas to our class as sometimes we will prefer to use the squared value and avoid a costly
square root function.

		float Vec2f::squaredMag()
		{
			return x * x + y * y;
		}

		float Vec2f::mag()
		{
			return sqrt(squaredMag());
		}
				

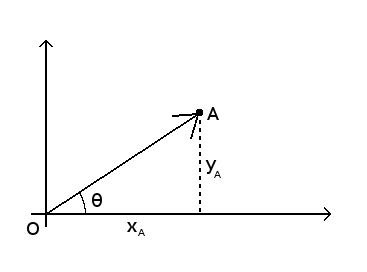
The argument of a vector is the angle between this vector and the horizontal axis.


From the trigonometric definitions we have:
$\tan \theta =\frac{y_A}{x_A}$
So we can get the angle:
$\theta =\arctan \frac{y_A}{x_A}$
In the code we will use the atan2 function to avoid problems like a division by 0.

		float Vec2f::arg()
		{
			return atan2(y, x);
		}
				

We will continue to add functions to this class in a future article.
You can download the code of this article here.

Frédéric Goset 2018