• Home
• 2D Geometry
• Contact

Vectors 2

This page displays mathematical formulas using a MathML script.
If you are reading this using Internet Explorer, I recommend you to accept the execution of this script when IE
asks it.

In the last article we saw how to get the angle between a vector and the horizontal axis.
Now we can do the opposite: setting the angle of a vector, keeping its length the same.
Following the rules of trigonometry, if we want to set the angle of a vector of length R we have to set its
coordinates to the values given in this image.


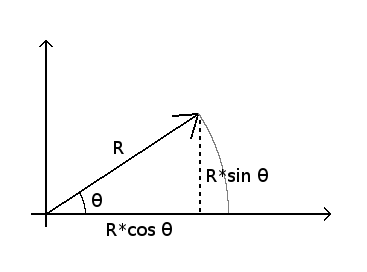
That leads to this code:

		void Vec2f::setAngle(const float angle)
		{
			float	R = mag();
			x = R * cos(angle);
			y = R * sin(angle);
		}
				

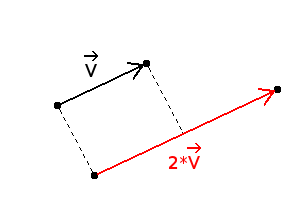
If we multiply a vector by a positive number it comes down to modifying its length.


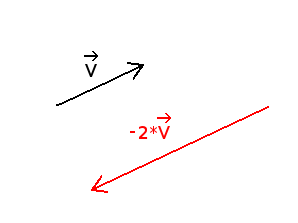
Multiplying it by a negative number also modifies its length, but reverts it too.


It is equivalent to multiplying each coordinate of the vector by the number.

		Vec2f Vec2f::operator*(const float m)
		{
			Vec2f   result;

			result.x = m * x;
			result.y = m * y;

			return result;
		}

		Vec2f& Vec2f::operator*=(const float m)
		{
			x *= m;
			y *= m;
			return *this;
		}
				

Dividing a vector by a number is quite the same as multiplying it.
It does not require more explanation.

		Vec2f Vec2f::operator/(const float m)
		{
			Vec2f   result;

			result.x = x / m;
			result.y = y / m;

			return result;
		}

		Vec2f& Vec2f::operator/=(const float m)
		{
			x /= m;
			y /= m;
			return *this;
		}
				

When we do calculations with vectors we often want to use vectors of length 1.
Reducing the length of a vector to 1 is an operation called normalization.
We simply have to divide the coordinates of the vector by its length.

		void Vec2f::normalize()
		{
			float	m = mag();
			*this /= m;
		}
				

If you refer to the image of the setAngle() function you will understand that the coordinates of a normalized
vector are simply the cosine and sine of its angle.

We usualy define two types of multiplications between 2 vectors: the dot product and the cross product.
The dot product - also called scalar product - of 2 vectors $\overrightarrow{u}$ and $\overrightarrow{v}$ is written $\overrightarrow{u}\cdot \overrightarrow{v}$.
Its result is a number defined as $x_u{x}_v+y_u{y}_v$.
That can be easily programmed:

		float Vec2f::dot(const Vec2f& a)
		{
			return x * a.x + y * a.y;
		}
				

The dot product also has another mathematical formulation:
$\overrightarrow{u}\cdot \overrightarrow{v}=\Vert \overrightarrow{u}\Vert \Vert \overrightarrow{v}\Vert \cos \theta$
where θ is the angle between $\overrightarrow{u}$ and $\overrightarrow{v}$.
This formulation leads to various usages in computer science.

First, if $\overrightarrow{u}$ and $\overrightarrow{v}$ are normalized, the product gives us the cosine of the angle between them
without having to calculate the angle itself.

If one of the vectors is normalized, say $\overrightarrow{v}$, the dot product give us the length of the projection of $\overrightarrow{u}$ on the line
that supports $\overrightarrow{v}$.


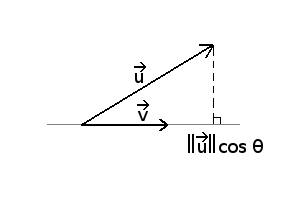
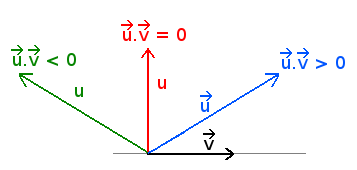
Even if the vectors are not normalized, looking at their product gives us informations on their relative position.

• If the product is positive, the vectors are in the "same" direction.
• If the product is zero the vectors are perpendicular.
• If the product is negative, the vectors are opposed.

The cross product of $\overrightarrow{u}$ and $\overrightarrow{v}$ is written $\overrightarrow{u}✗\overrightarrow{v}$.
Unlike the dot product the result is a vector, and specifically a 3D one.
In fact this vector is perpendicular to the 2 input vectors.
So in 2D its x and y coordinates are zero. We only use its z coordinate that is defined as:
$x_u{y}_v-y_u{x}_v$
That translates to this code:

		float Vec2f::cross(const Vec2f& a)
		{
			return x * a.y - y * a.x;
		}
				

As for the dot product, the cross product also has another mathematical notation:
$\overrightarrow{u}✗\overrightarrow{v}=\Vert \overrightarrow{u}\Vert \Vert \overrightarrow{v}\Vert \sin \theta \overrightarrow{k}$
Where θ is the angle from $\overrightarrow{u}$ to $\overrightarrow{v}$, and $\overrightarrow{k}$ is the unit vector along the z axis.

This formulations leads to various useful properties.
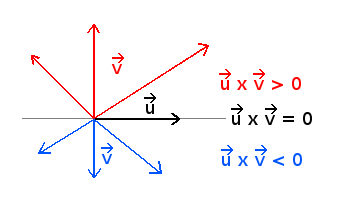
If the 2 vectors are normalized, the product is the sine of the angle between them.

The sign of the product tells us on which side of the line defined by $\overrightarrow{u}$ we can find $\overrightarrow{v}$.


In 2D the cross product can sometimes be used to compute distances, but it's mainly used to detect intersections
between lines.
It can also be used to tell the inside from the outside of a polygon.

Source code of the Vec2f class.

Frédéric Goset 2018