The code in this article was written using Code::Blocks and SDL 2.
You can read
here a guide to install this sofware.
Although it is based on SDL, I don't use its functions directly. I have written a small library with a few basic
functions to ease the understanding and the portability to another language.
You can read more about this lib
here.
In 1971 Thomas Schelling wrote a paper about the distribution of a population in a city.
The city is represented as a grid where each cell can be either empty or contain one of 2 types of "agents" - red
or green.
At each turn we select a random agent and a random empty cell.
The agent can decide to move to the empty cell or not.
Its decision is based on its neighborhood.
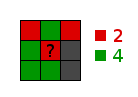
In the 8 neighbor cells, we count the number of agents of each color.
One of the parameters of the game is the coefficient of "likeness" of the agents.
Let's say that this coefficient is 30%.
Our agent will be "happy" if in its neigborhood there is at least 30% of agents that are the same color as him.
If our agent is unhappy in the current cell and if he would be happy in the empty one, then he will decide to move
to this cell.
After a while, the system should stabilize and even if the rules says that the agents are quite tolerant, we should
see that they clustered with other agents the same colors as them.
The population looks more segregated than mixed.
This simulation may look simple, but it's a good coding exercise, because it hides a few difficulties that are
typical to this type of games.
We will use a square grid of 30*30 cells.
#define NB_CELLS 30
#define CELL_SIZE (SCREEN_HEIGHT / NB_CELLS)
We will need the fraction of empty cells in the grid
#define EMPTY 0.1 // % of empty cells
The proportion of red cells
#define RED_RATIO 0.5 // % of red in the initial state
And the likeness coefficient
#define LIKENESS 0.3 // % of wanted neighbors of the same color
The grid will be stored in an int table that can contain 0 for an empty cell, 1 for a red agent or 2 for a green
one.
int grid[NB_CELLS][NB_CELLS];
// initialize the grid
for (int y = 0; y < NB_CELLS; y++)
for (int x = 0; x < NB_CELLS; x++)
grid[x][y] = 0;
And we will use a palette for these 3 values.
// initialize the palette
Color palette[3];
palette[0] = Color( 70, 70, 70); // empty cell
palette[1] = Color(220, 0, 0); // red
palette[2] = Color( 0, 150, 0); // green
To display the board, I wrote a function to draw a filled rectangle
void CGfx::rectFill(int x0, int y0, int x1, int y1, Color c)
{
for (int y = y0; y < y1; y++)
for (int x = x0; x < x1; x++)
gfx.setPixel(x, y, c);
}
I wrote a function for empty rectangles too, but we won't use it.
Now let's try to display our grid.
// draw the grid
for (int y = 0; y < NB_CELLS; y++)
for (int x = 0; x < NB_CELLS; x++)
{
gfx.rectFill( x * CELL_SIZE, y * CELL_SIZE,
(x + 1) * CELL_SIZE - 2, (y + 1) * CELL_SIZE - 2,
palette[grid[x][y]]);
}
Download source code
Download executable for Windows
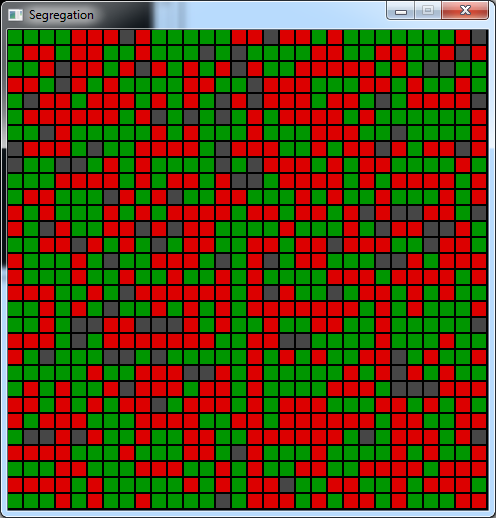
This gives us this result:
Then how do we fill this grid following the ratio of empty cells and the ratio of red/green cells ?
Let's say we have a red/green ratio of 50/50 and 10% of the grid is empty.
If we first fill the whole grid with red and green cells following the 50/50, and then we "empty" 10% of the
cells randomly, we can't be sure that the 50/50 is still observed.
So we'll start with an empty grid and we'll fill only the number of occupied cells, that is:
int nbOccupied = NB_CELLS * NB_CELLS * (1 - EMPTY); // number of occupied cells
Now, how do we fill the occupied cells by respecting the red/green ratio.
If we choose randomly the color of the cell we add we can't be sure that the final ratio will be good.
So we have to compute how many red cells we need:
int nbRed = nbOccupied * RED_RATIO; // number of red cells
And as we will fill nbOccupied cells, the first nbRed ones will be red. The other ones will be green.
We just need to add a loop to choose cells randomly until we find an empty one.
for (int i = 0; i < nbOccupied; i++)
{
// find an empty cell
while (true)
{
int x = rand() % NB_CELLS;
int y = rand() % NB_CELLS;
if (grid[x][y] == 0)
{
// fill the cell
if (i < nbRed)
grid[x][y] = 1;
else
grid[x][y] = 2;
break;
}
}
}
Download source code
Download executable for Windows
This code produces the same result as the first image of this article.
Now we will randomly select an empty cell
// find an empty cell
int xEmpty, yEmpty;
while (true)
{
xEmpty = rand() % NB_CELLS;
yEmpty = rand() % NB_CELLS;
if (grid[xEmpty][yEmpty] == 0)
break;
}
And an occupied one
// find an occupied cell
int xOccupied, yOccupied;
while (true)
{
xOccupied = rand() % NB_CELLS;
yOccupied = rand() % NB_CELLS;
if (grid[xOccupied][yOccupied] != 0)
break;
}
Now, to decide if the agent will move to the the empty cell, we will need to compute its "happiness" in the both
cells.
So we will write another function to count the neighbors of a cell.
The function to count the neighbors will take as parameters the coordinates of the cell and the color of the agent
we selected.
We need to pass the color because when we will count the neighbors of the empty cell we won't be able to retrieve
it easily.
The aim of the function will be to count the number of neighbors of the same color and of the opposite colors.
And it will return the ratio we will compare to the likeness coefficient.
float countNeighbors(int xCell, int yCell, int color)
{
// count neighbors
int nbSame = 0;
int nbOther = 0;
We will loop from -1 to 1 on both axes and add these values to the cell coordinates to get the coordinates of the
neighbors.
But we won't take into account the cell itself - when xi = 0 and yi = 0.
for (int yi = -1; yi <= 1; yi++)
for (int xi = -1; xi <= 1; xi++)
{
// don't count the center
if (xi == 0 && yi == 0)
continue;
int x = xCell + xi;
int y = yCell + yi;
We won't count cells that are outside the grid too.
// check if we are not outside of the grid
if (x < 0 || x >= NB_CELLS ||
y < 0 || y >= NB_CELLS)
continue;
And we won't count empty cells...
// empty cell ?
if (grid[x][y] == 0)
continue;
Then we can increase the counters
// count
if (grid[x][y] == color)
nbSame++;
else
nbOther++;
}
Now we can return the ratio. But be careful, it's not the ratio of nbSame over nbOther, but the ratio of nbSame
over the number of occupied neighbors, so (nbSame + nbOther):
return (float)nbSame / (float)(nbSame + nbOther);
But here there is another trap. We can't divide by zero, so we have to check that before returning:
if (nbSame + nbOther == 0)
return 0.0;
Back in the main loop after we chose the occupied and the empty cells, now we can decide if our agent need to move.
First we will compute it's current likeness:
// current likeness
int color = grid[xOccupied][yOccupied];
float likeOld = countNeighbors(xOccupied, yOccupied, color);
Then we can check if he is unhappy
// is unHappy ?
if (likeOld < LIKENESS)
{
If it's the case, we can compute the likeness he would have if he was in the empty cell
// new likeness
float likeNew = countNeighbors(xEmpty, yEmpty, color);
Then if he would be happy there, make it move.
// want to move ?
if (likeNew >= LIKENESS)
{
grid[xEmpty][yEmpty] = color;
grid[xOccupied][yOccupied] = 0;
}
}
Download source code
Download executable for Windows
This code tends to give the result described at the beginning.
But it gets slower and slower and we don't even know when it's finished.
We'll try to solve these problems right now.
The previous program slows down because it randomly choose an agent, then tries to see if he can move.
But this agent will only have a chance to move if it is unhappy. And as the program goes on, less and less agents
are unhappy.
So we will change the way the program works.
In the main loop, for each frame we will fill a table that will tell if each agent is happy.
At the same time we will count the number of unhappy agents and the mean likeness.
bool happy[NB_CELLS][NB_CELLS];
[...]
// fill happy table
int nbUnhappy = 0;
float meanLikeness = 0.0;
for (int y = 0; y < NB_CELLS; y++)
for (int x = 0; x < NB_CELLS; x++)
{
happy[x][y] = true;
if (grid[x][y] != 0)
{
float like = countNeighbors(x, y, grid[x][y]);
meanLikeness += like;
if (like < LIKENESS)
{
happy[x][y] = false;
nbUnhappy++;
}
}
}
printf("likeness: %f%% unhappy: %f%%\n", meanLikeness * 100.0 / (float)nbOccupied, (float)nbUnhappy * 100.0 / (float)nbOccupied);
This way we will know when the program ends because the number of unhappy agents will get to 0.
Then instead of picking a random agent, we will choose an unhappy one.
// find an unhappy cell
int xOccupied, yOccupied;
while (true)
{
xOccupied = rand() % NB_CELLS;
yOccupied = rand() % NB_CELLS;
if (happy[xOccupied][yOccupied] == false)
break;
}
And the decision process will then be simpler:
// new likeness
int color = grid[xOccupied][yOccupied];
float likeNew = countNeighbors(xEmpty, yEmpty, color);
// want to move ?
if (likeNew >= LIKENESS)
{
grid[xEmpty][yEmpty] = color;
grid[xOccupied][yOccupied] = 0;
}
Download source code
Download executable for Windows
This code looks faster even if I increased the grid to 40*40 and I added a sys.wait(50) in the main loop !
Yet we do a lot more calculations each frame because we count the neighbors for every agent instead of only the one
we selected.
But that the sort of things that happens when an algorithm uses random choices. Sometimes doing more calculations
to reduce the randomness can be profitable.
There are other techniques to speed up this code even more. I'll perhabs talk about that in another article.
And now we have another advantage: we can tell if the program really ended by looking at the number of unhappy
agents.
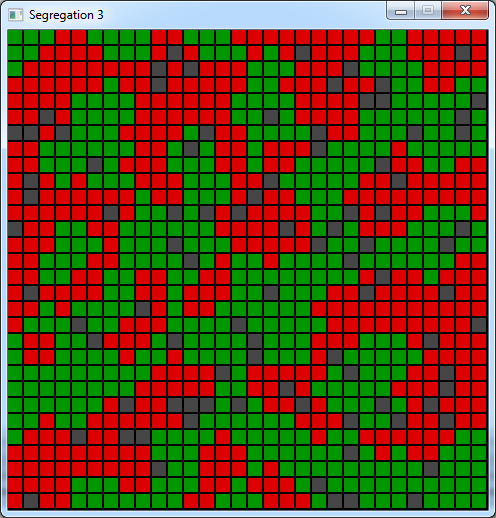
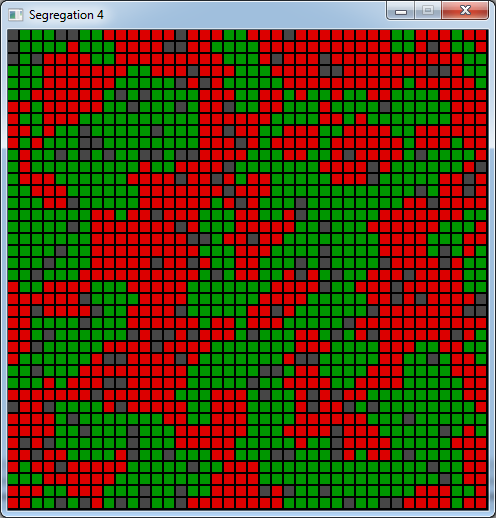
With the parameters we chose this number goes down to 0 after a while. And this is an example of the final state of
the board:
We can clearly see the clustering. At the end, the average likeness is around 75%, when each agent only wanted a
minimum of 30% !
Now let's play with the parameters to see what happens.
If we set the red ratio to 0.3, the percentage of unhappy agent will probably not go beyond 6%.
Because it's harder for red to find suitable places while the greens don't want to move because they are happy
where they live.
That's probably another lesson to learn if you want to be a mayor: no matter what you do, there will probably
be some people that will never be happy of their neighborhood.
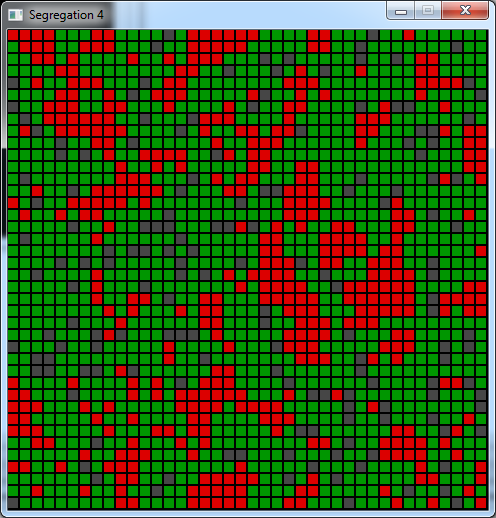
Here is an example of what we get when the program stabilizes:
If we get back to 50% of red and set the likeness coefficient to 0.5, we get an even clearer segregation.
With a likeness coefficient of 0.6 another interesting behavior appears: the empty cells are ordered to act as
"walls" between the 2 groups. Here we reach an average likeness of 96%.
Adding a 3rd color to this simulation is not difficult.
Let's say we'll add blue agents.
First we will need a palette entry for this new color:
palette[3] = Color( 20, 20, 255); // blue
Then we need the ratio that we will use to fill the starting grid:
#define RED_RATIO 0.333 // % of red in the initial state
#define BLUE_RATIO 0.333 // % of blue in the initial state
[...]
int nbOccupied = NB_CELLS * NB_CELLS * (1 - EMPTY); // number of occupied cells
int nbRed = nbOccupied * RED_RATIO; // number of red cells
int nbBlue = nbOccupied * BLUE_RATIO; // number of blue cells
for (int i = 0; i < nbOccupied; i++)
{
// find an empty cell
while (true)
{
int x = rand() % NB_CELLS;
int y = rand() % NB_CELLS;
if (grid[x][y] == 0)
{
// fill the cell
if (i < nbRed)
grid[x][y] = 1;
else if (i < nbRed + nbBlue)
grid[x][y] = 3;
else
grid[x][y] = 2;
break;
}
}
}
Download source code
Download executable for Windows
And that's all.
Here is the result:



 Video: Lecture about this simulation at University of Michigan
Video: Lecture about this simulation at University of Michigan