Note to Internet Explorer users
This page displays mathematical formulas using a MathML script.
If you are reading this using Internet Explorer, I recommend you to accept the execution of this script when IE
asks it.
The code in this article was written using Code::Blocks and SDL 2.
You can read
here a guide to install this software.
Although it is based on SDL, I don't use its functions directly. I have written a small library with a few basic
functions to ease the understanding and the portability to another language.
You can read more about this lib
here.
A reaction-diffusion system is a simulation of the evolution of one or more chemical substances.
One substance system are not very interesting. So we will simulate one with 2 substances.
Alan Turing was the first to use these sytems to explain how patterns appears on animals coats.
But many scientists continued his work and came out with simpler equations.
Here we will use the Gray-Scott model.
Specifically we will try to reproduce the
Coding Train video and to speed up the code to a usable level.
So to simulate this, each pixel of the screen will contain the concentrations of A and B.
These values will stay between 0 and 1.
At each time step we will update the concentrations in each pixel using these formulas:
Where:
- At and Bt are the current concentrations
- At+1 and Bt+1 are the concentrations at the next time step
- Δt is a time coefficient. We will use 1, so you can forget it.
- DA and DB are diffusion rates. And the strange triangle after is the laplacian of the corresponding
concentration.
- f is the feeding rate of substance A
- k is the killing rate of substance B
Now lets explain this a little bit. There are 3 parts inside the parentheses.
The 3rd part says that substance A will be fed in the system at a rate "f", while substance b will be killed at a
rate "k".
The second part "AB
2" says that 2 "atoms" of B will react with an "atom" of A and convert it to a B.
The first part, with the strange triangle is the diffusion part. It says at which rate the substances will spread
out to the neighboring pixels.
The laplacian is a kind of 2D derivative. We can approximate it with a convolution.
That means we will take the current pixel and its 8 neighbours, and we will sum them with weights following this
matrix:
In this article we will use the same values as in the video:
- DA = 1
- DB = 0.5
- f = 0.055
- k = 0.062
In another article we will see what we can get if we change these values.
Now let's program these equations.
We will store the 2 concentrations per pixel in an array:
float table[2][SCREEN_HEIGHT][SCREEN_WIDTH];
We will use another array to store the results of the computations for the next frame:
float nextTable[2][SCREEN_HEIGHT][SCREEN_WIDTH];
Then we define our constants.
float DA = 1.0f;
float DB = 0.5f;
float f = 0.055f;
float k = 0.062f;
We will have a function to compute the laplacian:
float Laplacian(int tab, int x, int y)
{
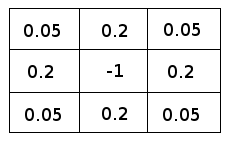
Here is the weights matrix:
static const float coef[3][3] =
{
{0.05f, 0.2f, 0.05f},
{0.2f, -1.0f, 0.2f},
{0.05f, 0.2f, 0.05f}
};
We start 2 loops going from -1 to 1, because we want to go one pixel to the left and to the right, and one pixel
above/below.
float sum = 0;
for (int dy = -1; dy <= 1; dy++)
for (int dx = -1; dx <= 1; dx++)
{
We calculate the coordinates of the pixel, wrapping it around if we get out of the screen.
int posX = (x + dx + SCREEN_WIDTH) % SCREEN_WIDTH;
int posY = (y + dy + SCREEN_HEIGHT) % SCREEN_HEIGHT;
We get the coefficient from the array and add the value of this pixel to the sum.
float c = coef[dy + 1][dx + 1];
sum += c * table[tab][posY][posX];
}
And finally, we return the sum
return sum;
}
An update function will compute the formulas we saw above.
void update()
{
We loop through each pixel:
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
We get the current A and B concentrations:
float A = table[0][y][x];
float B = table[1][y][x];
And we apply the formulas to the nextTable:
nextTable[0][y][x] = A + DA * Laplacian(0, x, y) - A * B * B + f * (1.0f - A);
nextTable[1][y][x] = B + DB * Laplacian(1, x, y) + A * B * B - (k + f) * B;
}
Finally we copy the content of nextTable to table to be ready for the next frame.
memcpy(table, nextTable, SCREEN_WIDTH * SCREEN_HEIGHT * 2 * sizeof(float));
}
In the main() function, we will initialize the table full of A:
// initialize the table
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
table[0][y][x] = 1.0f;
table[1][y][x] = 0.0f;
}
With a small square of B at the center:
for (int y = 0; y < 10; ++y)
for (int x = 0; x < 10; ++x)
{
int posX = SCREEN_WIDTH / 2 + x - 5;
int posY = SCREEN_HEIGHT / 2 + y - 5;
table[1][posY][posX] = 1.0f;
}
Then in the main loop we will display the content of the table, using red for A and blue for B:
while (sys.isQuitRequested() == false)
{
// draw the current table
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
Color col(table[0][y][x] * 255,
0,
table[1][y][x] * 255);
gfx.setPixel(x, y, col);
}
We handle the system events:
gfx.render();
sys.processEvents();
And finally we call our update function:
// update the table
update();
}
Download source code
Download executable for Windows
As you will see, this program is quite slow.
If you are patient, once it filled the screen you will see that:
Like every time you want to optimize a program, you must first look at the time your code takes.
We will use the same timing functions we used for the metaballs.
But if you try to time each frame separately you will see that the result increases every time.
So we will rather add the times of the 2000 first frames to get a more stable value.
We will use 2 variables. "tim" will store the sum of the times and "cnt" will be a simple counter of the frame
number.
float tim = 0;
int cnt = 0;
At the beginning of update() we will start the timer:
sys.StartPerfCounter();
And at the end of this function, we will increase the counter, add the times and display the result at the 2000th
frame:
cnt++;
if (cnt < 2000)
tim += sys.StopPerfCounter();
else if (cnt == 2000)
printf("%f\n", tim);
Download source code
Download executable for Windows
The value we get is about 45000 ms.
When I optimize a code I usualy try to replace the floats with ints.
It's an habit i got from working on old computers and game consoles.
In this particular program we can't use integers. I tried with different precisions and each time the reaction
stopped quickly.
So I tried to use doubles instead of floats and the result surprised me.
Here is the code when you replace all the floats with doubles, except for the timer variable.
#include <stdio.h>
#include <stdlib.h>
#include "main.h"
#include "Graphics.h"
#include "System.h"
#include <string.h>
#include <stdlib.h>
#define SCREEN_WIDTH 400
#define SCREEN_HEIGHT 400
double table[2][SCREEN_HEIGHT][SCREEN_WIDTH];
double nextTable[2][SCREEN_HEIGHT][SCREEN_WIDTH];
double DA = 1.0;
double DB = 0.5;
double f = 0.055;
double k = 0.062;
double Laplacian(int tab, int x, int y)
{
static const double coef[3][3] =
{
{0.05, 0.2, 0.05},
{0.2, -1.0, 0.2},
{0.05, 0.2, 0.05}
};
double sum = 0;
for (int dy = -1; dy <= 1; dy++)
for (int dx = -1; dx <= 1; dx++)
{
int posX = (x + dx + SCREEN_WIDTH) % SCREEN_WIDTH;
int posY = (y + dy + SCREEN_HEIGHT) % SCREEN_HEIGHT;
double c = coef[dy + 1][dx + 1];
sum += c * table[tab][posY][posX];
}
return sum;
}
float tim = 0;
int cnt = 0;
void update()
{
sys.StartPerfCounter();
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
double A = table[0][y][x];
double B = table[1][y][x];
nextTable[0][y][x] = A + DA * Laplacian(0, x, y) - A * B * B + f * (1.0 - A);
nextTable[1][y][x] = B + DB * Laplacian(1, x, y) + A * B * B - (k + f) * B;
}
memcpy(table, nextTable, SCREEN_WIDTH * SCREEN_HEIGHT * 2 * sizeof(double));
cnt++;
if (cnt < 2000)
tim += sys.StopPerfCounter();
else if (cnt == 2000)
printf("%f\n", tim);
}
int main(int argc, char* argv[])
{
// init the window
gfx.init("Reaction/Diffusion 2", SCREEN_WIDTH, SCREEN_HEIGHT);
gfx.init2D();
gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));
// initialize the table
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
table[0][y][x] = 1.0;
table[1][y][x] = 0.0;
}
for (int y = 0; y < 10; ++y)
for (int x = 0; x < 10; ++x)
{
int posX = SCREEN_WIDTH / 2 + x - 5;
int posY = SCREEN_HEIGHT / 2 + y - 5;
table[1][posY][posX] = 1.0;
}
while (sys.isQuitRequested() == false)
{
// draw the current table
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
Color col(table[0][y][x] * 255,
0,
table[1][y][x] * 255);
gfx.setPixel(x, y, col);
}
gfx.render();
sys.processEvents();
// update the table
update();
}
gfx.quit();
return EXIT_SUCCESS;
}
Download source code
Download executable for Windows
I always thought that float were a little bit faster than doubles taking into account the memory accesses, but I
was wrong.
This code takes only around 14000 ms !
Apparently on modern PC processors doubles are highly optimized.
I compared the assembly language generated by the compiler for the 2 versions, but I could not find anything to
explain that.
But some trick that worked with floats don't work with doubles. Its a whole new world of optimizations.
Now I will need to revisit some other programs on my website...
We gained a lot of time, but we can still do better.
The Laplacian() function probably takes most of the time of this program.
And thanks to its symmetries we can certainly write it in a more efficient way.
To reduce the multiplications, we can add together all the pixels that have a coefficient of 0.05, then all the
pixels that have a coefficient of 0.2.
And finally we will add all these partial sums using their weights.
We will use arrays to precompute the coordinates and make things clearer:
double Laplacian(int tab, int x, int y)
{
int xp[3];
int yp[3];
for (int i = -1; i <= 1; i++)
{
xp[i + 1] = (x + i + SCREEN_WIDTH) % SCREEN_WIDTH;
yp[i + 1] = (y + i + SCREEN_HEIGHT) % SCREEN_HEIGHT;
}
Then we can compute our sums:
double sum1 = table[tab][yp[0]][xp[0]] +
table[tab][yp[0]][xp[2]] +
table[tab][yp[2]][xp[0]] +
table[tab][yp[2]][xp[2]];
double sum2 = table[tab][yp[0]][xp[1]] +
table[tab][yp[1]][xp[0]] +
table[tab][yp[1]][xp[2]] +
table[tab][yp[2]][xp[1]];
return 0.05 * sum1 + 0.2 * sum2 - table[tab][yp[1]][xp[1]];
}
Download source code
Download executable for Windows
This code takes only 9000 ms.
The calculations we do to "wrap" the coordinates when we are outside the screen uses the modulus operator "%".
But this operator takes the same time as a division. And a division is very expensive.
So we will remove these calculations. But to avoid getting out of the screen when we are calculating the laplacian
we will add 1 cell in each direction in our tables.
So their width and height will be increased by 2:
double table[2][SCREEN_HEIGHT+2][SCREEN_WIDTH+2];
double nextTable[2][SCREEN_HEIGHT+2][SCREEN_WIDTH+2];
The coordinates in the laplacian are now simply:
for (int i = -1; i <= 1; i++)
{
xp[i + 1] = x + i;
yp[i + 1] = y + i;
}
And we also have to change the loops in the update() function:
for (int y = 1; y < SCREEN_HEIGHT+1; ++y)
for (int x = 1; x < SCREEN_WIDTH+1; ++x)
{
double A = table[0][y][x];
The memcpy():
memcpy(table, nextTable, (SCREEN_WIDTH+2) * (SCREEN_HEIGHT+2) * 2 * sizeof(double));
In the initialisation we need to set the values of nextTable too, to avoid black borders around the image.
// initialize the table
for (int y = 0; y < SCREEN_HEIGHT+2; ++y)
for (int x = 0; x < SCREEN_WIDTH+2; ++x)
{
table[0][y][x] = 1.0;
table[1][y][x] = 0.0;
nextTable[0][y][x] = 1.0;
nextTable[1][y][x] = 0.0;
}
And of course the drawing routine changes too:
// draw the current table
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
int r = table[0][y+1][x+1] * 255;
int b = table[1][y+1][x+1] * 255;
gfx.setPixel(x, y, Color(r, 0, b));
}
Download source code
Download executable for Windows
This code only needs about 6000 ms for the 2000 first frames.
Of course we don't get the same image when the screen is filled:
But we will find a way to reimplement the wrapping later.
Rewriting the laplacian (2)
There is a much clever way to rewrite the Laplacian() function.
A convolution can be seen as the multiplication of a matrix by the pixels of the screen.
This matrix has symmetries and it can nearly be written as a product of 2 simpler matrices.
Let's try.
Now if we mutiply that by 0.05:
We get nearly the same matrix we wanted except for the central element.
But as we use the sum of all these elements, it will be easy to substract 1.8 * table[t][y][x] afterwards to get
the "-1" coefficient we want.
So we can break the convolution down to 2 successive ones.
The fact that there is an horizontal matrix and a vertical one means that one of the convolution is applied in the
x direction while the other will be along the y direction.
We will compute these operations for each pixel of the screen and store them into 2 new arrays:
double prod1Table[2][SCREEN_HEIGHT+2][SCREEN_WIDTH+2];
double prod2Table[2][SCREEN_HEIGHT+2][SCREEN_WIDTH+2];
Here is the function we will use to fill these tables:
void product()
{
for (int t = 0; t < 2; t++)
{
for (int y = 0; y < SCREEN_HEIGHT+2; ++y)
for (int x = 1; x < SCREEN_WIDTH+1; ++x)
prod1Table[t][y][x] = table[t][y][x - 1] + 4.0f * table[t][y][x] + table[t][y][x + 1];
for (int y = 1; y < SCREEN_HEIGHT+1; ++y)
for (int x = 1; x < SCREEN_WIDTH+1; ++x)
prod2Table[t][y][x] = prod1Table[t][y - 1][x] + 4.0f * prod1Table[t][y][x] + prod1Table[t][y + 1][x];
}
}
The Laplacian() function now simply uses the result of these calculations. Here we substract the value for the
center of the matrix.
double Laplacian(int tab, int x, int y)
{
return 0.05 * prod2Table[tab][y][x] - 1.8 * table[tab][y][x];
}
Now we only have to call product() in the update() function before everything else:
void update()
{
sys.StartPerfCounter();
product();
Download source code
Download executable for Windows
This version takes 3000 ms.
Rewriting the main formulas
I made some tests on the main formulas. Trying to find a way to compute them more efficiently.
Here are the results of my investigations.
Our current formulas look like that:
nextTable[0][y][x] = A + DA * Laplacian(0, x, y) - A * B * B + f * (1.0 - A);
nextTable[1][y][x] = B + DB * Laplacian(1, x, y) + A * B * B - (k + f) * B;
Now that the laplacian is a simple formula, we can replace it in these ones:
nextTable[0][y][x] = A + DA * (0.05 * prod2Table[0][y][x] - 1.8 * table[0][y][x]) - A*B*B + f*(1.0 - A);
nextTable[1][y][x] = B + DB * (0.05 * prod2Table[1][y][x] - 1.8 * table[1][y][x]) + A*B*B - (k + f)*B;
We can replace table[0][y][x] and table[1][y][x] by their values of A and B:
nextTable[0][y][x] = A + DA * (0.05 * prod2Table[0][y][x] - 1.8*A) - A*B*B + f*(1.0 - A);
nextTable[1][y][x] = B + DB * (0.05 * prod2Table[1][y][x] - 1.8*B) + A*B*B - (k + f)*B;
If we expand the parentheses:
nextTable[0][y][x] = A + DA * 0.05 * prod2Table[0][y][x] - 1.8*DA*A - A*B*B + f - f*A;
nextTable[1][y][x] = B + DB * 0.05 * prod2Table[1][y][x] - 1.8*DB*B + A*B*B - k*B - f*B;
Now if we regroup the terms that contains A and B:
nextTable[0][y][x] = 0.05 * DA * prod2Table[0][y][x] - A*B*B + A - f*A - 1.8*DA*A + f;
nextTable[1][y][x] = 0.05 * DB * prod2Table[1][y][x] + A*B*B + B - f*B - 1.8*DB*B - k*B;
Now we factorize A and B:
nextTable[0][y][x] = 0.05 * DA * prod2Table[0][y][x] - A*B*B + (1.0 - f - 1.8*DA) * A + f;
nextTable[1][y][x] = 0.05 * DB * prod2Table[1][y][x] + A*B*B + (1.0 - f - 1.8*DB - k) * B;
Or if we introduce 2 new variables for the factors of A and B:
double ca = 1.0 - f - 1.8 * DA;
double cb = 1.0 - f - 1.8 * DB - k;
nextTable[0][y][x] = 0.05 * DA * prod2Table[0][y][x] - A*B*B + ca * A + f;
nextTable[1][y][x] = 0.05 * DB * prod2Table[1][y][x] + A*B*B + cb * B;
Notice that these 2 variables only use values that are constants across all pixels.
So we can set them out of the loops.
Now the update() function looks like this:
void update()
{
sys.StartPerfCounter();
double ca = 1.0 - f - 1.8 * DA;
double cb = 1.0 - f - 1.8 * DB - k;
product();
for (int y = 1; y < SCREEN_HEIGHT+1; ++y)
for (int x = 1; x < SCREEN_WIDTH+1; ++x)
{
double A = table[0][y][x];
double B = table[1][y][x];
nextTable[0][y][x] = 0.05 * DA * prod2Table[0][y][x] - A * B * B + ca * A + f;
nextTable[1][y][x] = 0.05 * DB * prod2Table[1][y][x] + A * B * B + cb * B;
}
[...]
}
Download source code
Download executable for Windows
This program need around 2600 ms.
To avoid copying tables, we will get rid of nextTable and add a dimension to table:
double table[2][2][SCREEN_HEIGHT+2][SCREEN_WIDTH+2];
We will use a curT variable to tell which table is the current one:
int curT = 0;
In the product() function only one line will change:
prod1Table[t][y][x] = table[curT][t][y][x - 1] + 4.0f * table[curT][t][y][x] + table[curT][t][y][x + 1];
And the update() function will now look like this:
void update()
{
[...]
for (int y = 1; y < SCREEN_HEIGHT+1; ++y)
for (int x = 1; x < SCREEN_WIDTH+1; ++x)
{
double A = table[curT][0][y][x];
double B = table[curT][1][y][x];
table[1-curT][0][y][x] = 0.05 * DA * prod2Table[0][y][x] - A * B * B + ca * A + f;
table[1-curT][1][y][x] = 0.05 * DB * prod2Table[1][y][x] + A * B * B + cb * B;
}
The memcpy() will be replaced with a simple variable flipping:
curT = 1 - curT;
Download source code
Download executable for Windows
And of course the initialization and the drawing parts changes too but I won't bother you with that.
This code takes about 2200 ms on my i7-4770K. That's more than 20 times faster than the first one.
Putting back the wrapping
If we want to get back the wrapping around the screen we removed at the beginning, we simply have to "fill" the
extra pixels all around the screen with a copy of the opposite visible ones.
void update()
{
double ca = 1.0 - f - 1.8 * DA;
double cb = 1.0 - f - 1.8 * DB - k;
for (int t = 0; t < 2; ++t)
{
for (int x = 0; x < SCREEN_WIDTH + 2; ++x)
{
table[curT][t][SCREEN_HEIGHT - 1][x] = table[curT][t][1][x];
table[curT][t][0][x] = table[curT][t][SCREEN_HEIGHT - 2][x];
}
for (int y = 0; y < SCREEN_HEIGHT + 2; ++y)
{
table[curT][t][y][SCREEN_WIDTH - 1] = table[curT][t][y][1];
table[curT][t][y][0] = table[curT][t][y][SCREEN_WIDTH - 2];
}
table[curT][t][0][0] = table[curT][t][SCREEN_HEIGHT - 2][SCREEN_WIDTH - 2];
table[curT][t][0][SCREEN_WIDTH - 1] = table[curT][t][SCREEN_HEIGHT - 2][1];
table[curT][t][SCREEN_HEIGHT - 1][0] = table[curT][t][1][SCREEN_WIDTH - 2];
table[curT][t][SCREEN_HEIGHT - 1][SCREEN_WIDTH - 1] = table[curT][t][1][1];
}
Download source code
Download executable for Windows
Even when the screen is filled, the pattern continues to evolve.
But it's rather hard to see.
So we will "light up" the evolution using green.
We simply have to set the green value of the pixels to something depending on the difference between the current
and the next table:
int r = table[0][0][y+1][x+1] * 255;
int b = table[0][1][y+1][x+1] * 255;
int g = (table[0][0][y+1][x+1] - table[1][0][y+1][x+1]) * 650000;
g = ABS(g);
if (g > 255)
g = 255;
gfx.setPixel(x, y, Color(r, g, b));
Download source code
Download executable for Windows
Here is what we see when it runs:



 Video: Reaction Diffusion in JavaScript
Video: Reaction Diffusion in JavaScript