Bresenham's circle algorithm

Another circle

In a previous article I talked about a way to draw a circle using trigonometric functions:

		 $x = x_{C} + r * cos θ$ 

		 $y = y_{C} + r * sin θ$

Where

(x_{C}, y_{C})

are the coordinates of the center and r is the radius.
This time we will use another formula to describe a circle.
Remember that by definition, a circle is the set of points that are at a given distance of the center.
This distance is the radius.
Using the Pythagorean theorem we can write:

		 ${(x - x_{C})}^{2} + {(y - y_{C})}^{2} = r^{2}$

Or by taking the square root:

		 $\sqrt{{(x - x_{C})}^{2} + {(y - y_{C})}^{2}} = r$

Now let's assume that our circle is centered at (0, 0).
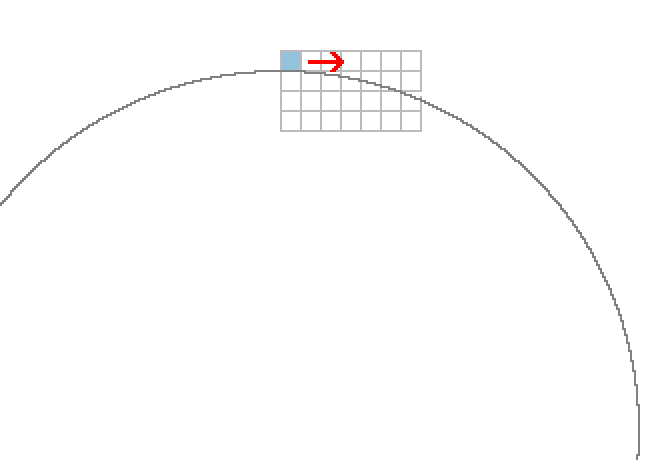
Imagine that we are at the top of the circle, where (x, y) = (0, r).
We will increase x towards the right.

The point will tend to move away from the center.
So at each x coordinate we will compute

\sqrt{x^{2} + y^{2}}

.
And if it's greater than r, we will go down one pixel.
These are the red arrows in this image:

We will stop when x = y.
When we draw our pixel we just have to add the coordinates of the center and the code will look like that:

		int cX = SCREEN_WIDTH  / 2;
		int cY = SCREEN_HEIGHT / 2;
		int r = 150;

		int x = 0;
		int y = r;

		while (x <= y)
		{
			gfx.setPixel(cX + x, cY + y, Color(255, 255, 255));

			x++;

			if (sqrt(x * x + y * y) > r)
				y--;
		}
		
		Download source code
		Download executable for Windows

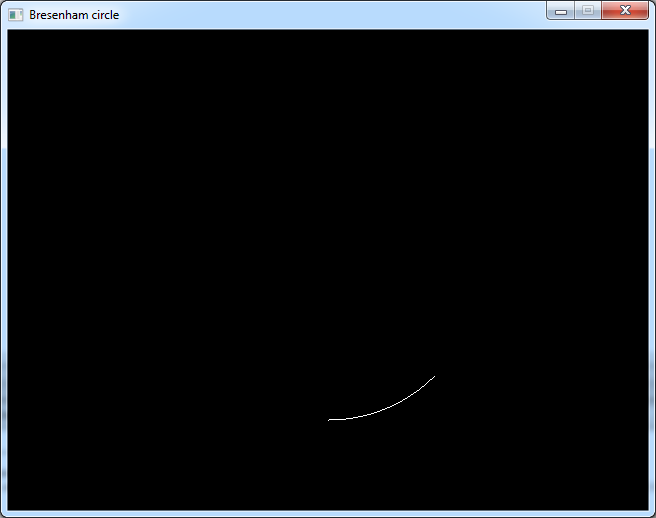
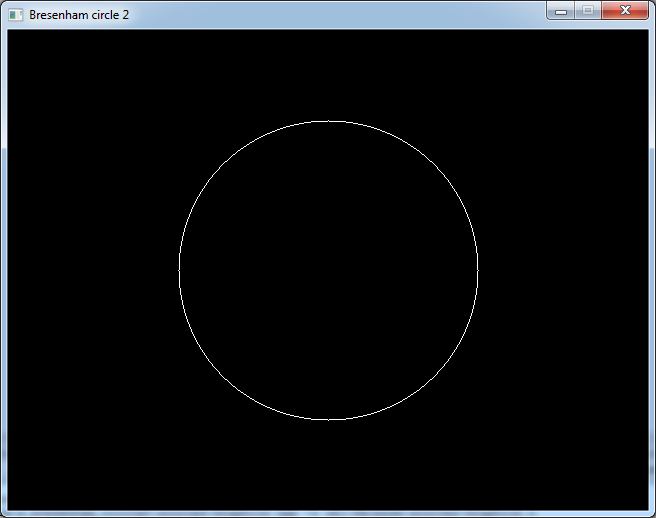
And this is the result.
Notice that we drew the bottom part of the circle because with screen coordinates the Y axis increases towards the
bottom.

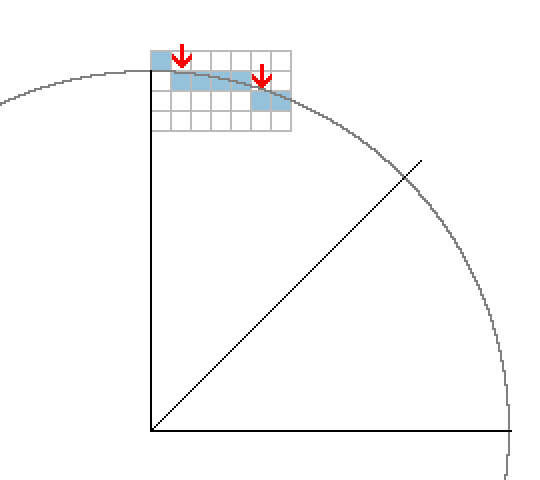
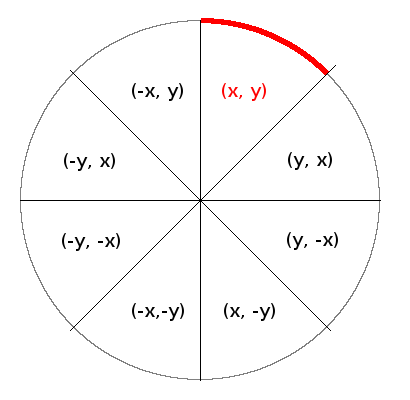
Now we only drew one eighth of the circle: the red one in the image below.
But we can take advantage of the symmetries of the circle to draw the other parts by simply manipulating the
coordinates:

This is what we will change in the code:

		while (x <= y)
		{
			gfx.setPixel(cX + x, cY + y, Color(255, 255, 255));
			gfx.setPixel(cX + x, cY - y, Color(255, 255, 255));
			gfx.setPixel(cX - x, cY + y, Color(255, 255, 255));
			gfx.setPixel(cX - x, cY - y, Color(255, 255, 255));
			gfx.setPixel(cX + y, cY + x, Color(255, 255, 255));
			gfx.setPixel(cX + y, cY - x, Color(255, 255, 255));
			gfx.setPixel(cX - y, cY + x, Color(255, 255, 255));
			gfx.setPixel(cX - y, cY - x, Color(255, 255, 255));

			x++;

			if (sqrt(x * x + y * y) > r)
				y--;
		}
		
		Download source code
		Download executable for Windows

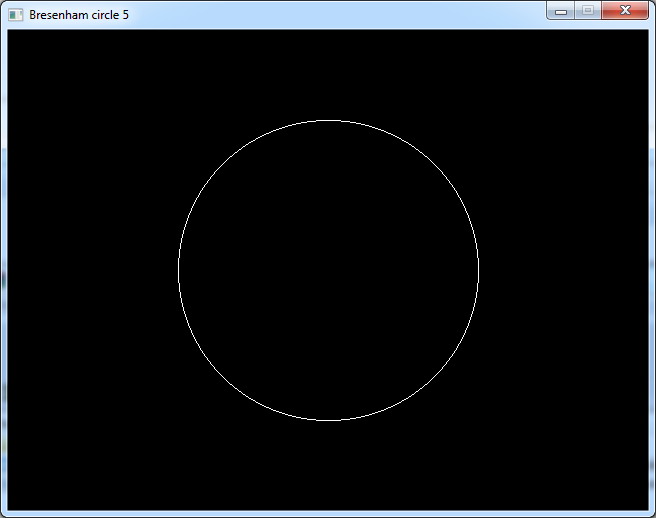
And now we can see the full circle.

Timing

We saw the basic idea of how to draw the circle.
But as it was the case for the line, the Bresenham algorithm is more about optimising this basic idea.
So to see the effects of these optimisations better, we will time the algorithm.
Firstly we will put it in a function:

		void circle(int centerX, int centerY, int radius, Color c)
		{
			int x = 0;
			int y = radius;

			while (x <= y)
			{
				gfx.setPixel(centerX + x, centerY + y, c);
				gfx.setPixel(centerX + x, centerY - y, c);
				gfx.setPixel(centerX - x, centerY + y, c);
				gfx.setPixel(centerX - x, centerY - y, c);
				gfx.setPixel(centerX + y, centerY + x, c);
				gfx.setPixel(centerX + y, centerY - x, c);
				gfx.setPixel(centerX - y, centerY + x, c);
				gfx.setPixel(centerX - y, centerY - x, c);

				x++;

				if (sqrt(x * x + y * y) > radius)
					y--;
			}
		}

Then for more precision, we will time 10000 calls of this function.

		// time 10000 circles
		sys.StartPerfCounter();

		for (int i = 0; i < 10000; i++)
			circle(SCREEN_WIDTH  / 2, SCREEN_HEIGHT / 2, 150, Color(255, 255, 255));

		printf("%f\n", sys.StopPerfCounter());
		
		Download source code
		Download executable for Windows

This code takes about 33 ms on my computer.

Tweaking the coordinates

In the previous programs we implicitely defined that the integer coordinates are on the boundaries between 2
pixels.
That causes some imperfections. If you look at the uppermost pixel for example, it seems that it is alone on its
line. ASll the other pixels are at least one line below.

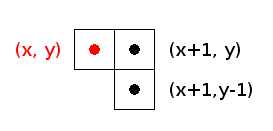
The classical Bresenham algorithm instead considers that the coordinates represents the center of a pixel.
Let's say we are at the point (x, y). The next point we will draw will be either the one at the right (x+1, y), or
the one below it (x+1, y-1)

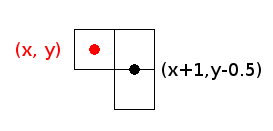
We will test only one point between these two, at coordinates (x+1, y-0.5).

As before we will check if:

		 $\sqrt{x^{2} + y^{2}} > r$

But we will modify it a little bit.
Firstly, the square root is an expensive operation. So we can as well check the squared values:

		 $x^{2} + y^{2} > r^{2}$

Then, to get closer to the original algorithm, we will subtract r² from both sides:

		 $x^{2} + y^{2} - r^{2} > 0$

The code at the end of the loop now looks like:

		float X = x + 1;
		float Y = y - 0.5f;
		float m = X * X + Y * Y - radius * radius;

		x++;

		if (m > 0)
			y--;

		Download source code
		Download executable for Windows

This code is not really faster, but it produces a circle a little bit rounder.

Using integers

Integer calculations are faster than floating point ones.
But the equations we use are not really integer friendly.
So let's rework them. We have:

		 $X = x + 1$ 

		 $Y = y - 0.5$ 

		 $m = X^{2} + Y^{2} - r^{2}$

If we replace X and Y in the 3rd equation we get:

		 $m = {(x + 1)}^{2} + {(y - 0.5)}^{2} - r^{2}$

Now if we expand that:

		 $m = x^{2} + 2 x + 1 + y^{2} - y + 0.25 - r^{2}$ 

		 $m = x^{2} + y^{2} + 2 x - y - r^{2} + 1.25$

Now let's multiply everything by 4:

		 $4 m = 4 (x^{2} + y^{2} + 2 x - y - r^{2}) + 5$

Let's call this value "M".
As x, y and r are integers, M is also an integer.
And as we only tested if m was greater than 0, the result would be the same if we test 4m > 0 or M > 0.
So our code will now look like:

		int m = 4 * (x*x + y*y + 2*x - y - radius*radius) + 5;

		x++;

		if (m > 0)
			y--;

		Download source code
		Download executable for Windows

This version takes about 10 ms.

Incrementation

Like the line algorithm the core principle of the circle one is to increment an error value for each pixel we draw.
Here "m" can be considered as our error value.
For now it is recomputed at every step from the values of x, y and r.
But we can imagine to set it to a starting value and we will add to it a given value every time we increase x,
and add another value every time we decrease y.

This explanation may be confusing. So let's see that in the code.
At the moment our loop look like that:

		int x = 0;
		int y = radius;

		while (x <= y)
		{
			[draw pixels]

			int m = 4 * (x*x + y*y + 2*x - y - radius*radius) + 5;

			x++;

			if (m > 0)
				y--;
		}

We want to change it so that it looks like that:

		int x = 0;
		int y = radius;
		int m = m_start;

		while (x <= y)
		{
			[draw pixels]

			if (m > 0)
			{
				m += m_inc_y;
				y--;
			}

			m += m_inc_x;
			x++;
		}

And we only need to find the values of m_start, m_inc_x and m_inc_y.

So let's try to find m_inc_x.
At the current point we have:

		 $m = 4 (x^{2} + y^{2} + 2 x - y - r^{2}) + 5$

If we increase x by 1, we have:

		 $m' = 4 ({(x + 1)}^{2} + y^{2} + 2 (x + 1) - y - r^{2}) + 5$

Let's work on that:

		 $m' = 4 (x^{2} + 2 x + 1 + y^{2} + 2 x + 2 - y - r^{2}) + 5$ 

		 $m' = 4 (x^{2} + y^{2} + 2 x - y - r^{2}) + 5 + 4 (2 x + 1 + 2)$ 

		 $m' = m + 4 (2 x + 3)$ 

		 $m' = m + 8 x + 12$

		 $m_inc_x = 8 x + 12$

And our code becomes:

		int x = 0;
		int y = radius;
		int m = m_start;

		while (x <= y)
		{
			[draw pixels]

			if (m > 0)
			{
				m += m_inc_y;
				y--;
			}

			m += 8 * x + 12;
			x++;
		}

Alternately, we can increase "m" after increasing x. In this case we have:

		int x = 0;
		int y = radius;
		int m = m_start;

		while (x <= y)
		{
			[draw pixels]

			if (m > 0)
			{
				m += m_inc_y;
				y--;
			}

			x++;
			m += 8 * x + 4;
		}

Now for m_inc_y. When we decrease y by 1 we have:

		 $m' = 4 (x^{2} + {(y - 1)}^{2} + 2 x - (y - 1) - r^{2}) + 5$ 

		 $m' = 4 (x^{2} + y^{2} - 2 y + 1 + 2 x - y + 1 - r^{2}) + 5$ 

		 $m' = 4 (x^{2} + y^{2} + 2 x - y - r^{2}) + 5 + 4 (- 2 y + 1 + 1)$ 

		 $m' = m + 4 (- 2 y + 2)$ 

		 $m' = m - 8 y + 8$ 

		 $m_inc_y = - 8 y + 8$

That leads to this code:

		int x = 0;
		int y = radius;
		int m = m_start;

		while (x <= y)
		{
			[draw pixels]

			if (m > 0)
			{
				m += -8 * y + 8;
				y--;
			}

			x++;
			m += 8 * x + 4;
		}

Or if we increase m after decreasing y:

		int x = 0;
		int y = radius;
		int m = m_start;

		while (x <= y)
		{
			[draw pixels]

			if (m > 0)
			{
				y--;
				m -= 8 * y;
			}

			x++;
			m += 8 * x + 4;
		}

Now for m_start, as a reminder we have:

		 $m = 4 (x^{2} + y^{2} + 2 x - y - r^{2}) + 5$

And we are at the point of coordinates (0, radius).
So if we replace that in the equation, we get:

		 $m = 4 (0^{2} + r^{2} + 2 * 0 - r - r^{2}) + 5$ 

		 $m = 4 (r^{2} - r - r^{2}) + 5$ 

		 $m = -4 r + 5$

And the final code is:

		int x = 0;
		int y = radius;
		int m = 5 - 4 * radius;

		while (x <= y)
		{
			[draw pixels]

			if (m > 0)
			{
				y--;
				m -= 8 * y;
			}

			x++;

			m += 8 * x + 4;
		}

		Download source code
		Download executable for Windows

This is basically the same level of optimisation as the historical Bresenham's algorithm.
But although the computations inside the loop are far less complex than before, this version of the code is not
faster than the previous program on a modern PC.
That is probably because of the way the compiler optimizes the code and the way a modern processor works.

In the next article we will see how to draw filled circles from this algorithm, and how to optimise them.