The code in this article was written using Code::Blocks and SDL 2.
You can read
here a guide to install this software.
Although it is based on SDL, I don't use its functions directly. I have written a small library with a few basic
functions to ease the understanding and the portability to another language.
You can read more about this lib
here.
For this article I updated the complex numbers class
The
Newton's method is an algorithm to find zeroes of a function by applying repeatedly this formula:
xn+1 = xn - f(xn) / f'(xn)
Where f'(x) is the derivative of the function f(x).
To turn it into a fractal we need to apply that to complex numbers.
As for the Mandelbrot set the screen will represent the complex plane and each pixel will be a complex number.
And we will apply the formula until we reach a maximum number of iterations.
But like the Mandelbrot we can break out of this iteration loop if a condition is fulfilled.
For the Mandelbrot set it was when the value of z got too big.
But for a Newton fractal, most of the pixels will tend towards a zero of the function so we'll check when they get
near enough of one of these zeroes.
Typically for a a basic Newton fractal we use the function:
f(z) = z3 - 1
But we will see later that we can try with other functions.
We will also need its derivative:
f'(z) = 3z2
And we need to know its roots:
z1 = 1
z2 = -0.5 + i * √3 / 2
z3 = -0.5 - i * √3 / 2
On the
english Newton fractal wikipedia page there is a sample code chunk to draw it.
And we will turn it to a working program.
As for the Mandelbrot set we will need a maximum number of iterations and a limit value to get out of the loop.
#define MAX_ITERATIONS 100
#define TOLERANCE 1e-6
Then we define our function and its derivative.
// the function
Complex f(Complex z)
{
// z^3 - 1
static Complex one(1, 0);
return z * z * z - one;
}
// derivative of the function
Complex df(Complex z)
{
// 3 * z^2
return (z * z) * 3;
}
In the main function we will first define some value to tell where the window will be centered and what will be
its size according to the complex plane.
static double zoom = 2.0 / (double)SCREEN_HEIGHT;
static double centerX = (double)SCREEN_WIDTH / 2.0;
static double centerY = (double)SCREEN_HEIGHT / 2.0;
We will need the roots of the function:
// roots of the function
Complex roots[3];
roots[0] = Complex(1, 0);
roots[1] = Complex(-0.5, sqrt(3) / 2);
roots[2] = Complex(-0.5, -sqrt(3) / 2);
Each pixel will take a color according to the root we reached in the iteration loop.
So we will define a palette. But we will add a value ad the end for pixels that have not reach any root after the
max number of iterations.
// palette
static Color palette[4];
palette[0] = Color(255, 0, 0);
palette[1] = Color(0, 255, 0);
palette[2] = Color(0, 0, 255);
palette[3] = Color(0, 0, 0);
Now we will draw the fractal. So we begin a loop over each pixels of the screen:
// draw the fractal
for (int y = 0; y < SCREEN_HEIGHT; y++)
{
for (int x = 0; x < SCREEN_WIDTH; x++)
{
We convert the pixel's coordinates to a complex number:
// convert the pixel pos to a complex number
Complex z;
z.re = (x - centerX) * zoom - 0.75;
z.im = (y - centerY) * zoom;
We will use a variable to store the root we reached. By default it's on the last palette color.
// by default the pixel is black if the calculations fail
int color = 3;
We start the iteration loop
// iterate
int iter;
for (iter = 0; iter < MAX_ITERATIONS; iter++)
{
Here is the Newton's formula
z = z - f(z) / df(z);
We loop on every root in the array to check if we reached one
// are we near a root ?
for (int i = 0; i < 3; i++)
{
Complex delta = z - roots[i];
double distance = delta.squareMag();
If we reached a root, we store its number and we break out of the roots checking loop.
if (distance < TOLERANCE)
{
color = i;
break;
}
}
And we break out of the iteration loop too:
if (color != 3)
break;
}
And finally we draw the pixel.
// draw the pixel
gfx.setPixel(x, y, palette[color]);
As the drawing could take time, at the end of each line, we will render it and process the events to check if the
user closed the window. It's to avoid the program to seem unresponsive during the drawing.
}
gfx.render();
sys.processEvents();
if (sys.isQuitRequested() == true)
break;
}
At the end we add a loop to wait for the user to close the window if the drawing is done.
// wait until we quit
while (sys.isQuitRequested() == false)
{
sys.processEvents();
sys.wait(16);
}
gfx.quit();
return EXIT_SUCCESS;
Download source code
Download executable for Windows
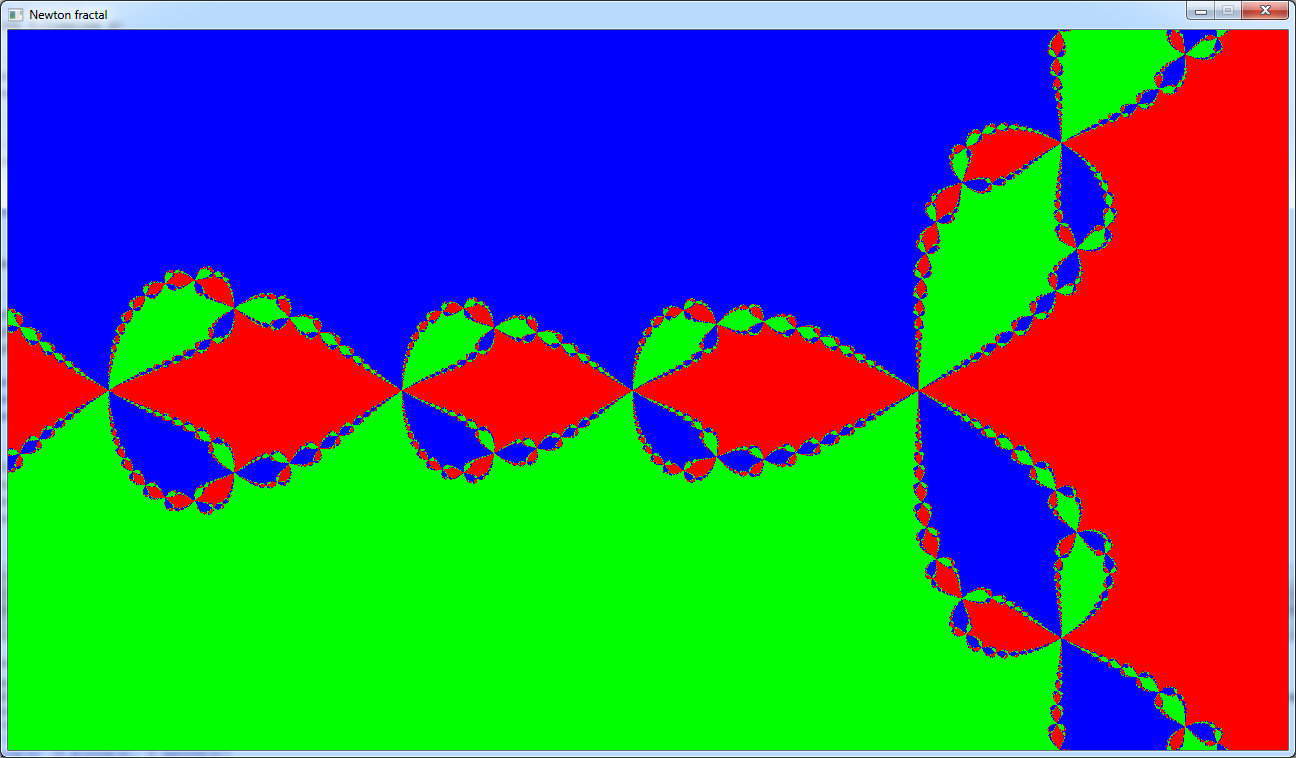
And this is the result:
This image looks a little bit flat.
So we will change the color of the pixel according to the number of iterations we did.
Note: I renamed the "color" variable to palIdx as it makes more sense.
Now before we draw the pixel, we will have this code:
// draw the pixel
Color color = palette[palIdx];
if (palIdx != 3)
{
float coef = 1 - log(iter + 1) / 5.0;
if (coef < 0)
coef = 0;
color.r *= coef;
color.g *= coef;
color.b *= coef;
}
gfx.setPixel(x, y, color);
Download source code
Download executable for Windows
I compute a coefficient from the logarithm of the number of iterations.
This coefficient should stay between 0 and 1.
Then I multiply the R, G, B values of the color by this coefficient.
The result is that the color will get darker when the number of iterations increases.
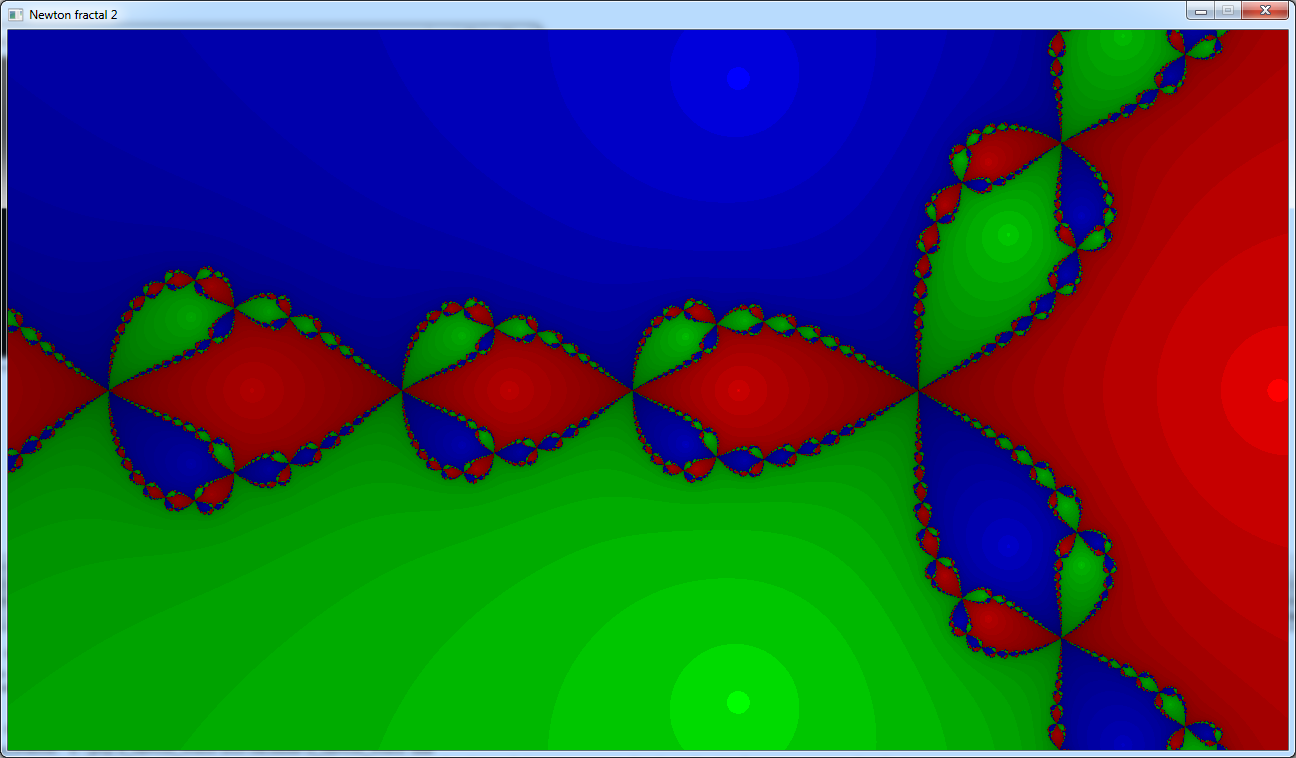
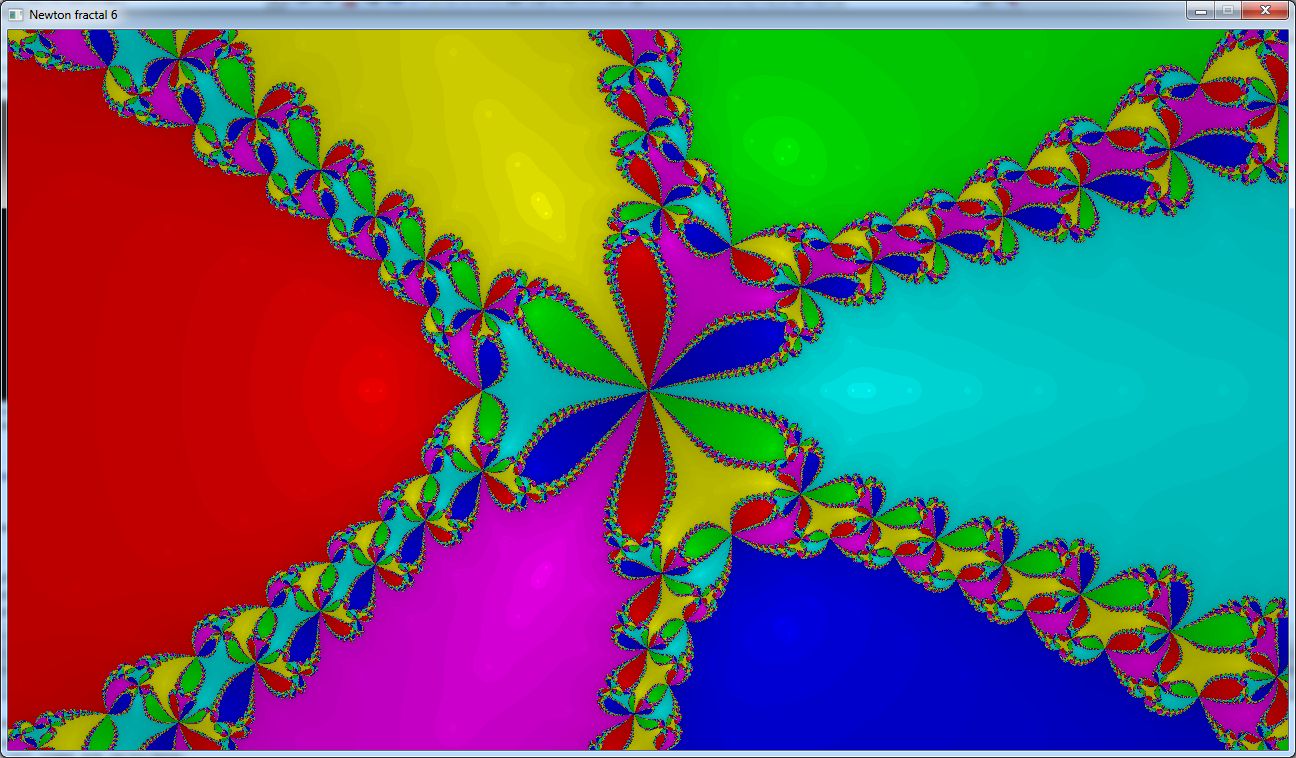
And this is the image that we get:
Now we can see the roots of the function.
These are the light dots that are in the wide areas outside the fractal.
Now I will try to reproduce most of the images you can see on the
Newton fractal wikipedia page.
We'll start with the z
3 - 2z + 2 image.
Now if you want to change the function in this code you also need its derivative and its root.
We'll see others methods to avoid that, but for now a quick visit to
Wolfram Alpha should give you all you need.
So this is what we need to change in the code:
// the function
Complex f(Complex z)
{
// z^3 - 2z + 2
return z * z * z - z * 2 + Complex(2, 0);
}
// derivative of the function
Complex df(Complex z)
{
// 3 * z^2 - 2
return (z * z) * 3 - Complex(2, 0);
}
[...]
// roots of the function
Complex roots[3];
roots[0] = Complex(-1.7693, 0);
roots[1] = Complex(0.88465, 0.58974);
roots[2] = Complex(0.88465, -0.58974);
Download source code
Download executable for Windows
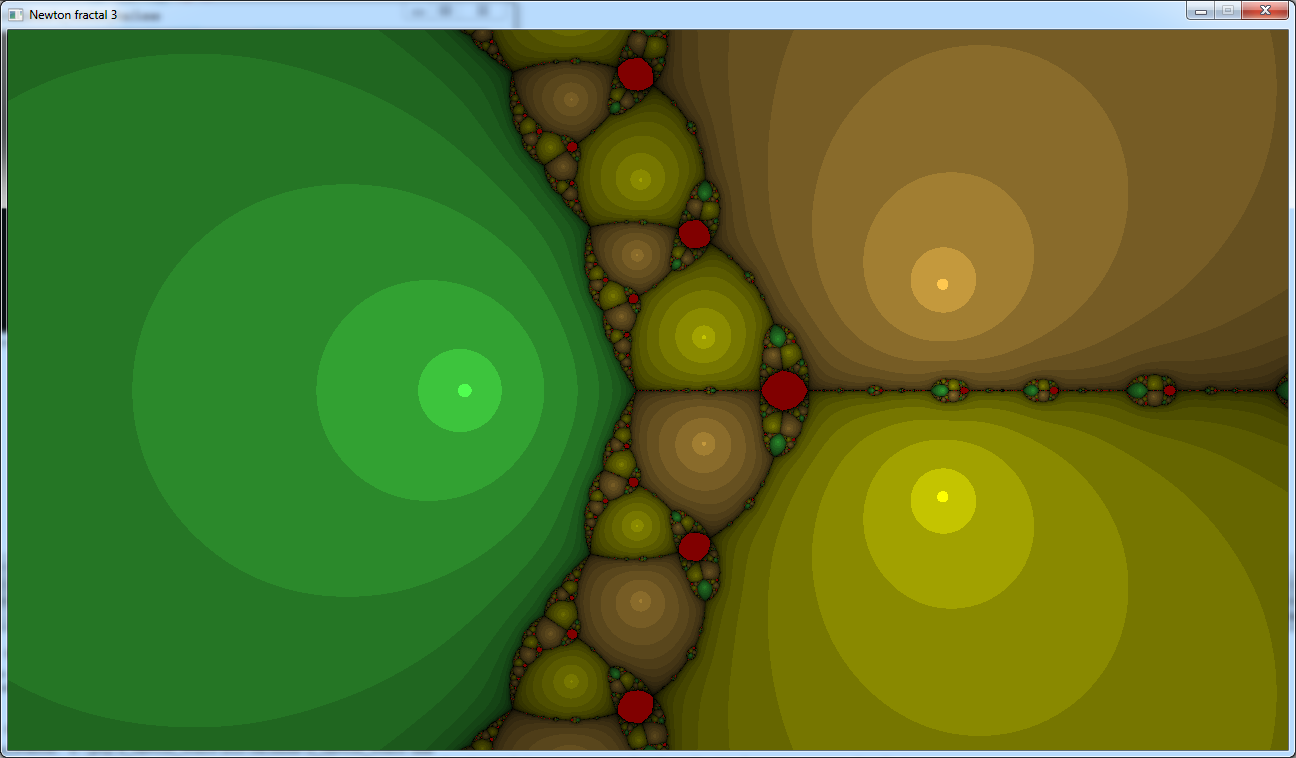
I also changed the colors and the shading coefficient to get closer than the source image, and this is what we get:
The peculiarity with this function is that for some starting values we don't get to a root.
These areas are in red on this image.
This one has more roots so it implies a few changes when we test the palIdx variable.
But apart from that there are not many changes.
// the function
Complex f(Complex z)
{
// z^8 + 15z^4 - 16
Complex z4 = z*z*z*z;
return z4 * z4 + z4 * 15 - Complex(16, 0);
}
// derivative of the function
Complex df(Complex z)
{
// 8z^7 + 60z^3
Complex z3 = z*z*z;
Complex z4 = z3 * z;
return (z4 * z3) * 8 + z3 * 60;
}
[...]
// roots of the function
Complex roots[8];
roots[0] = Complex(-1, 0);
roots[1] = Complex(1, 0);
roots[2] = Complex(0, -1);
roots[3] = Complex(0, 1);
roots[4] = Complex( 1.4142, 1.4142);
roots[5] = Complex(-1.4142, 1.4142);
roots[6] = Complex( 1.4142, -1.4142);
roots[7] = Complex(-1.4142, -1.4142);
Download source code
Download executable for Windows
f(z) = z5 - 3iz3 - (5+2i)z2 + 3z + 1
// the function
Complex f(Complex z)
{
// z^5 - 3iz^3 - (5+2i)z^2 + 3z + 1
return z * z * z * z * z - Complex(0, 3) * z * z * z - Complex(5, 2) * z * z + z * 3 + Complex(1, 0);
}
// derivative of the function
Complex df(Complex z)
{
// 5z^4 - 9iz^2 - (10+4i)z + 3
return z * z * z * z * 5 - Complex(0, 9) * z * z - Complex(10, 4) * z + Complex(3, 0);
}
[...]
// roots of the function
Complex roots[5];
roots[0] = Complex(-1.28992, -1.87357);
roots[1] = Complex(-0.824853, 1.17353);
roots[2] = Complex(-0.23744, 0.0134729);
roots[3] = Complex(0.573868, -0.276869);
roots[4] = Complex(1.77834, 0.963437);
Download source code
Download executable for Windows
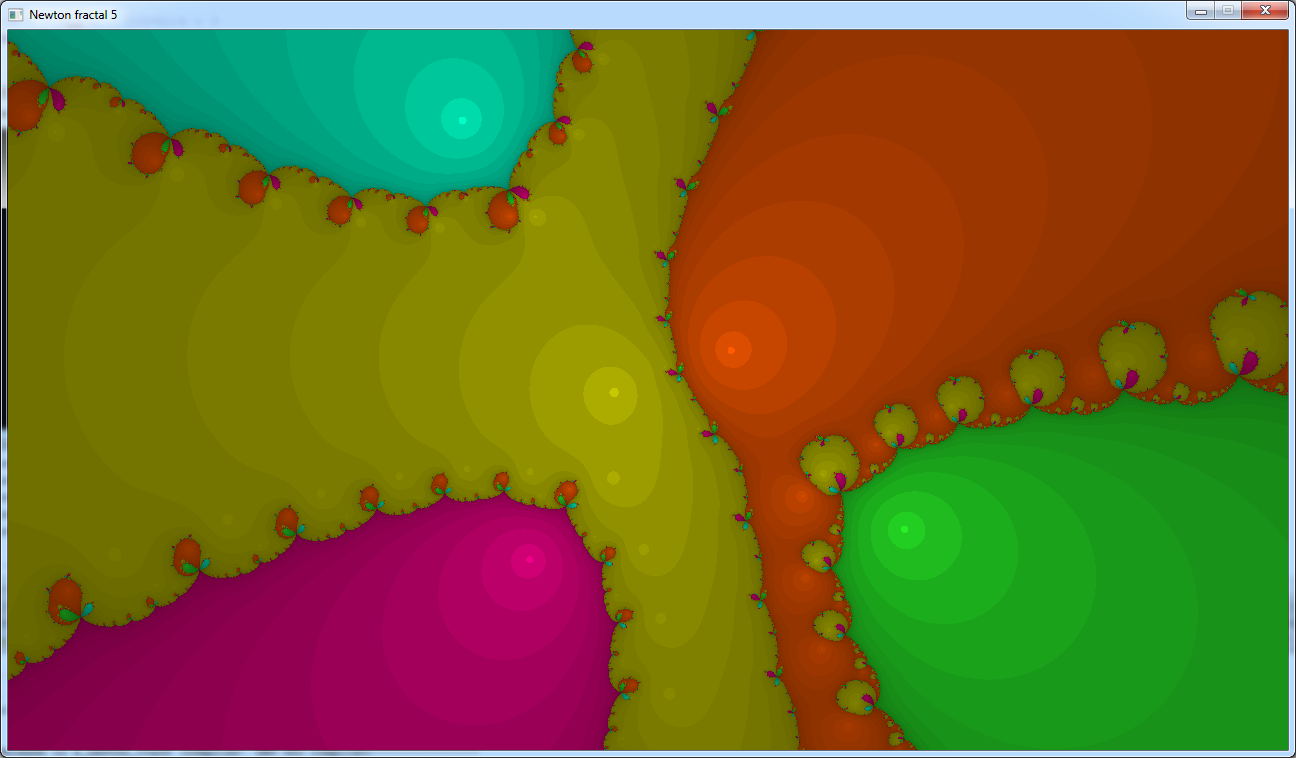
This one looks upside down compared with the image on wikipedia but the shape is the same.
// the function
Complex f(Complex z)
{
// z^6 + z^3 - 1
Complex z3 = z * z * z;
return z3 * z3 + z3 - Complex(1, 0);
}
// derivative of the function
Complex df(Complex z)
{
// 6z^5 + 3z^2
return z * z * z * z * z * 6 + z * z * 2;
}
[...]
// roots of the function
const int nbRoots = 6;
Complex roots[nbRoots];
roots[0] = Complex(-1.17398499670533, 0);
roots[1] = Complex(0.851799642079243, 0);
roots[2] = Complex(0.586992498352664, 1.016700830808605);
roots[3] = Complex(0.586992498352664, -1.016700830808605);
roots[4] = Complex(-0.425899821039621, -0.737680128975117);
roots[5] = Complex(-0.425899821039621, 0.737680128975117);
Download source code
Download executable for Windows
This one doesn't look as symetrical as the wikipedia one. I don't know why.
It's perhabs not the same part of the fractal.
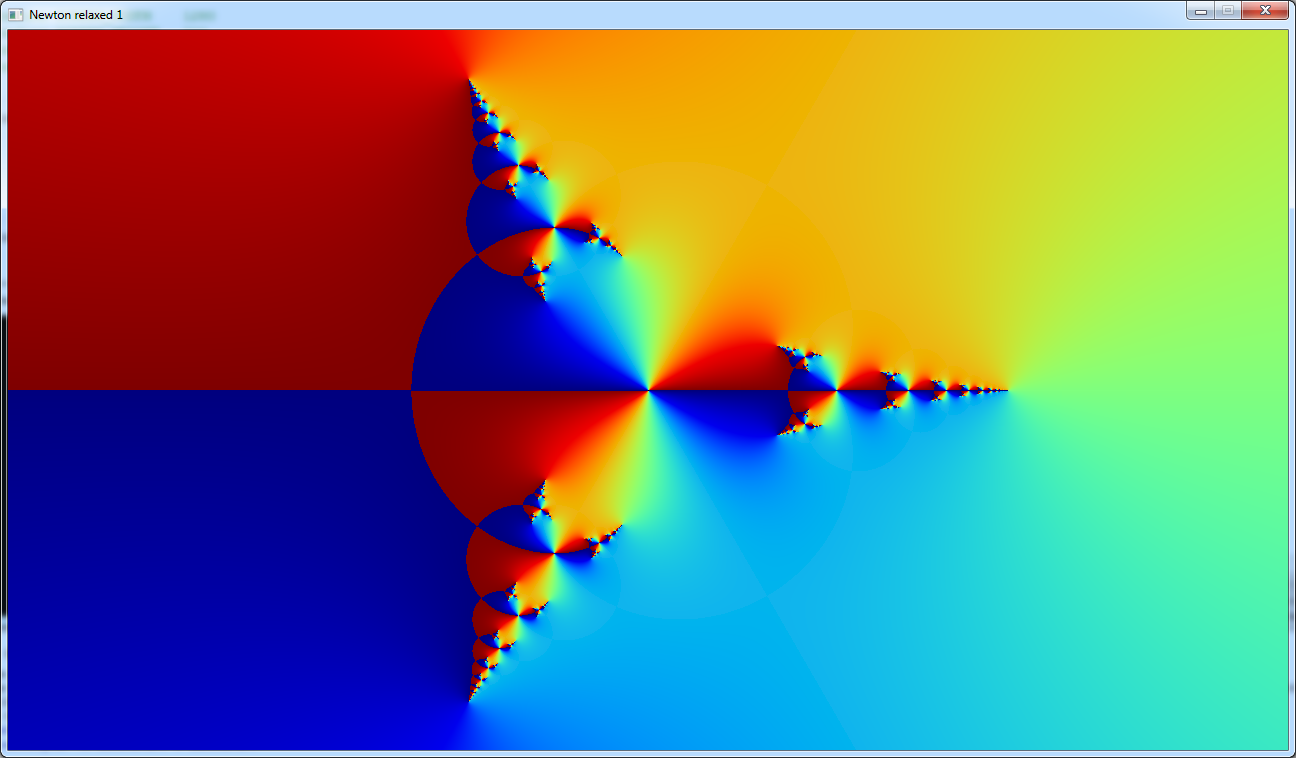
The english wikipedia page shows a variant of the formula where a coefficient is added:
zn+1 = zn - a * f(zn) / f'(zn)
With this formula the roots of the function don't match anymore.
So we won't use the roots or the palette in this code.
The first image that shows it uses a different coloring method.

By Asympt (talk) - self-made, Public Domain, Link
It uses the function z
3 - 1 with a = -0.5 and performs 40 iterations.
Then it takes the argument of z to find the color.
I tried to reproduce it exactly and it took me some time to find the right formulas for the color:
// draw the pixel
Color color;
color = Color(0, 0, 0);
float angle = z.arg();
if (angle <= M_PI / 3)
color.r = 127 + 128 * sin(-angle);
if (angle >= -M_PI * 2/3 && angle <= M_PI * 2/3)
color.g = 255 * sin(angle * 3/4 + M_PI / 2);
if (angle >= -M_PI / 3)
color.b = 127 + 128 * sin(angle);
gfx.setPixel(x, y, color);
Download source code
Download executable for Windows
And this is what I get:
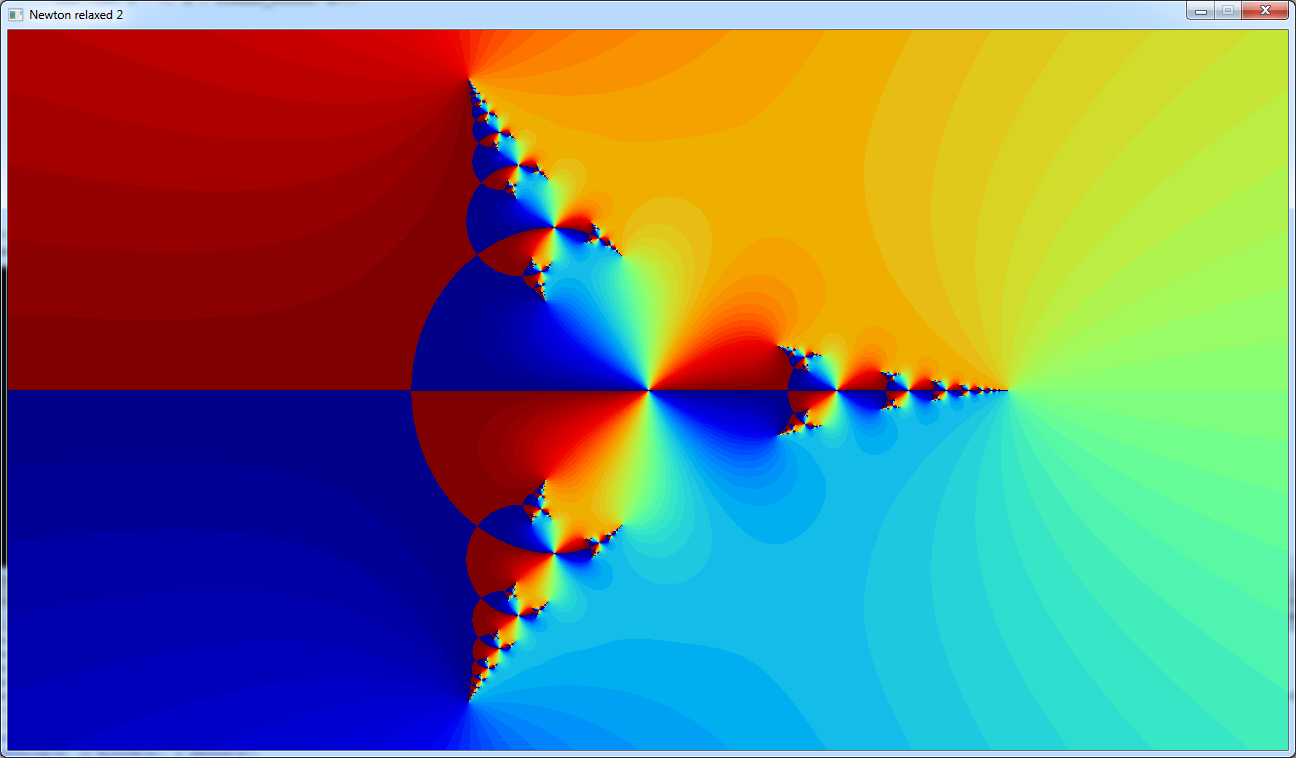
Now the original image has some banding because it uses a 64 colours palette.
We can reproduce that by "rounding" the angle:
float angle = z.arg();
angle = angle + M_PI;
angle = (int)(angle * 32 / M_PI);
angle = angle * M_PI / 32;
angle = angle - M_PI;
Download source code
Download executable for Windows
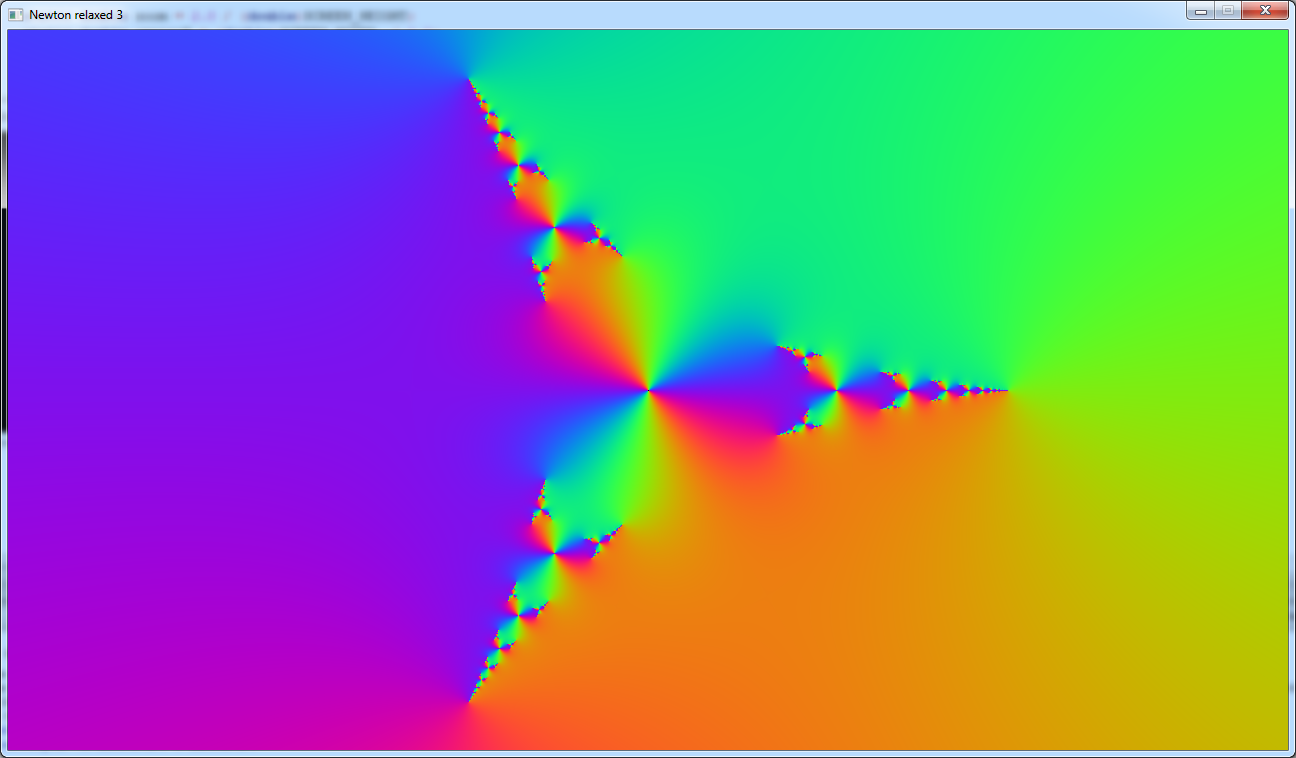
Then I tried a simpler colour scheme
// draw the pixel
Color color;
float angle = z.arg();
color.r = 127 * (1 + sin(angle));
color.g = 127 * (1 + sin(angle + 2 * M_PI / 3));
color.b = 127 * (1 + sin(angle + 4 * M_PI / 3));
gfx.setPixel(x, y, color);
Download source code
Download executable for Windows
And this is what I get:
That demonstrates that the aspect of a fractal can change a lot when you use a different palette.
f(z) = z2 - 1 ; a = 1 + i
Here are the changes for the second image using this variant.
// the function
Complex f(Complex z)
{
// z^2 - 1
return (z * z) - Complex(1, 0);
}
// derivative of the function
Complex df(Complex z)
{
// 2z
return z * 2;
}
[...]
Complex a(1, 1);
Download source code
Download executable for Windows
And for the 3rd image:
// the function
Complex f(Complex z)
{
// z^3 - 1
return (z * z * z) - Complex(1, 0);
}
// derivative of the function
Complex df(Complex z)
{
// 3z^2
return (z * z) * 3;
}
[...]
Complex a(2, 0);
Download source code
Download executable for Windows
The strange case of f(z) = sin(z)
Now let's get back to the standard Newton formula.
The image showing f(z) = sin(z) is a little bit trickier to obtain.
Writing the formulas is easy:
// the function
Complex f(Complex z)
{
// sin(z)
return Complex::Sin(z);
}
// derivative of the function
Complex df(Complex z)
{
// cos(z)
return Complex::Cos(z);
}
But this function has an infinite number of roots of the form n * π where n is an integer.
So this time again we will not use a root array nor a palette one.
But we will use a trick to find the root we reached.
First we divide z by π:
// are we near a root ?
Complex delta = z / Complex(M_PI, 0);
Then we compare this result with a complex created by taking the integer part of it:
Complex delta2 = delta - Complex((int)delta.re, 0);
double distance = delta2.squareMag();
if (distance < TOLERANCE)
{
Finally we can choose a color depending of this integer which is n:
found = true;
float n = (int)delta.re * 0.072345 * M_PI;
color.r = 127 * (1 + sin(n));
color.g = 127 * (1 + sin(n + 2 * M_PI / 3));
color.b = 127 * (1 + sin(n + 4 * M_PI / 3));
Download source code
Download executable for Windows
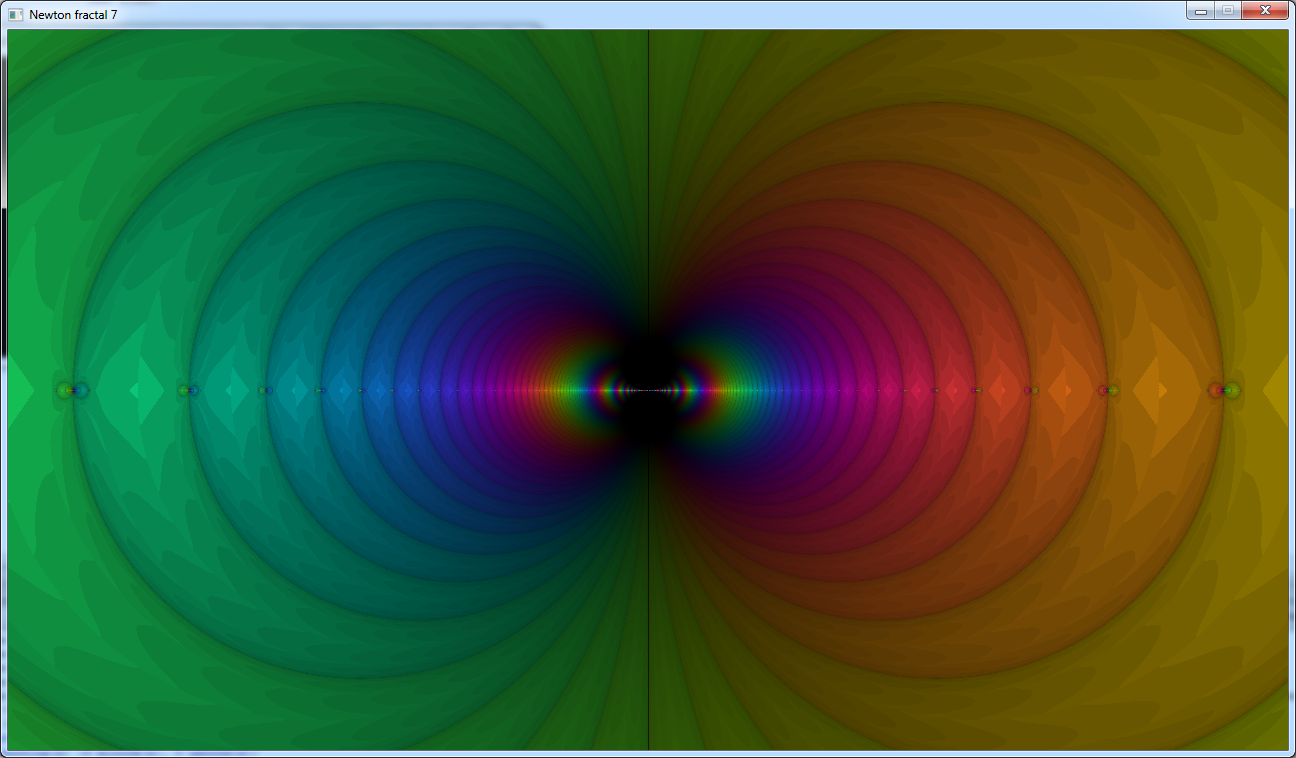
And after adding our shading coefficient we get this nice image:
Note that the 2 black circles here only appears because of our shading coefficient, but the fractal really has 2
black circles that appear when you zoom a little bit more.
The black vertical line in the center can probably disappear if you shift the complex coordinates of the window a
little bit.
The Newton method is not the only algorithm that mathematicians tried to find the roots of a function.
The french version of the
wikipedia page talks about some other variants.
The first one is the secant method where we replace the Newton formula with this one:
zn+1 = zn - f(zn) * (zn - zn-1) / (f(zn) - f(zn-1))
Here we don't need the derivative of the function but we need to use some tricks because the formula uses z
n-1.
This program and the following ones will be a modified version of the second program of this article.
Now instead of a simple "z" value we will have an array of 3 values:
// convert the pixel pos to a complex number
Complex z[3];
for (int i = 0; i < 3; i++)
{
z[i].re = (x - centerX) * zoom - 0.75 + (2-i) * TOLERANCE;
z[i].im = (y - centerY) * zoom;
}
Notice that we add a small value to the real part because the method will not work if z
n-1 is equal to z
n.
Then the iteration formula will look like this:
z[2] = z[1] - f(z[1]) * (z[1] - z[0]) / (f(z[1]) - f(z[0]));
z[0] = z[1];
z[1] = z[2];
Download source code
Download executable for Windows
And here is the image we get:
If you look at the several black areas, you can tell that this method is not very efficient to find a root of
z
3 - 1
The second variant described in the french page uses the Halley method:
zn+1 = zn - 2 * f(zn) * f'(zn) / (2 * [f'(zn)]2 - f(zn) * f''(zn))
It's a cubic method that uses the second derivative of the function.
// the function
Complex f(Complex z)
{
// z^3 - 1
static Complex one(1, 0);
return z * z * z - one;
}
// derivative of the function
Complex df(Complex z)
{
// 3 * z^2
return (z * z) * 3;
}
// second derivative of the function
Complex ddf(Complex z)
{
// 6 * z
return z * 6;
}
And the formula looks like that:
Complex fz = f(z);
Complex dz = df(z);
Complex ddz = ddf(z);
z = z - fz * dz * 2 / (dz * dz * 2 - fz * ddz);
Download source code
Download executable for Windows
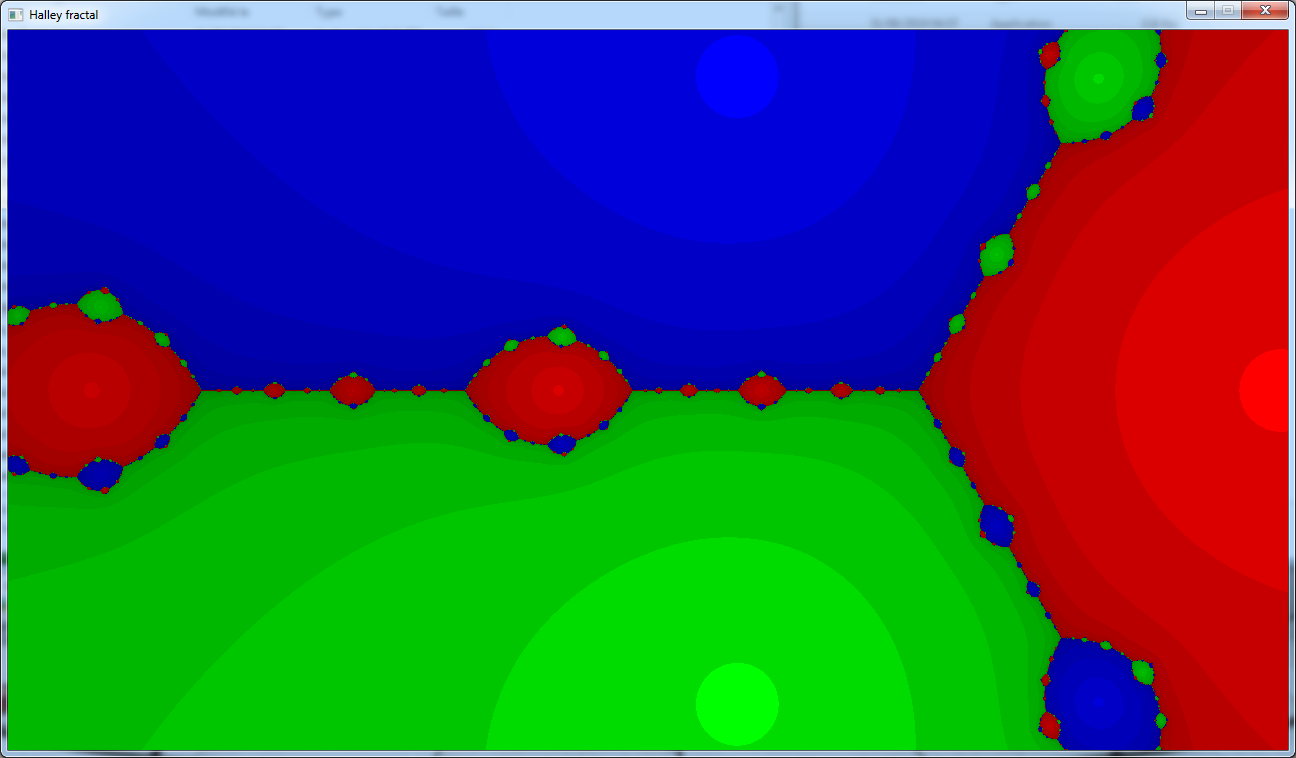
The result is a bit more boring than the classic Newton fractal:
The third variant presented in the french page is the Householder method.
It's a combination of the Newton and the Halley methods:
zn+1 = zn - (1 + h) * f(zn) / f'(zn)
Where
h = f(zn) * f''(zn) / (2 * [f'(zn)]2)
The formula is implemented like this:
Complex fz = f(z);
Complex dz = df(z);
Complex ddz = ddf(z);
Complex h = (fz * ddz) / (dz * dz * 2);
z = z - (Complex(1, 0) + h) * fz / dz;
Download source code
Download executable for Windows
And the result is a little bit more interesting:
The english page talks about a Nova fractal without giving examples of it.
The formula is an extension of the first variant we saw.
We not only introduce an "a" coefficient but we add a constant too:
zn+1 = zn - a * f(zn) / f'(zn) + c
The iteration will now look like this:
// iterate
int iter;
Complex a(1, 0);
Complex c(0.3, 0.3);
for (iter = 0; iter < MAX_ITERATIONS; iter++)
{
Complex oldZ = z;
z = z - a * f(z) / df(z) + c;
Now, as before we can't rely on the roots of the original function, so we will use the same argument coloring
technique.
But the formula tends to converge towards a root anyways.
So instead of running a fixed amount iterations, I break out of the loop when the difference between z
n+1 and z
n
is small enough:
Complex delta = z - oldZ;
double distance = delta.squareMag();
if (distance < TOLERANCE)
break;
}
Download source code
Download executable for Windows
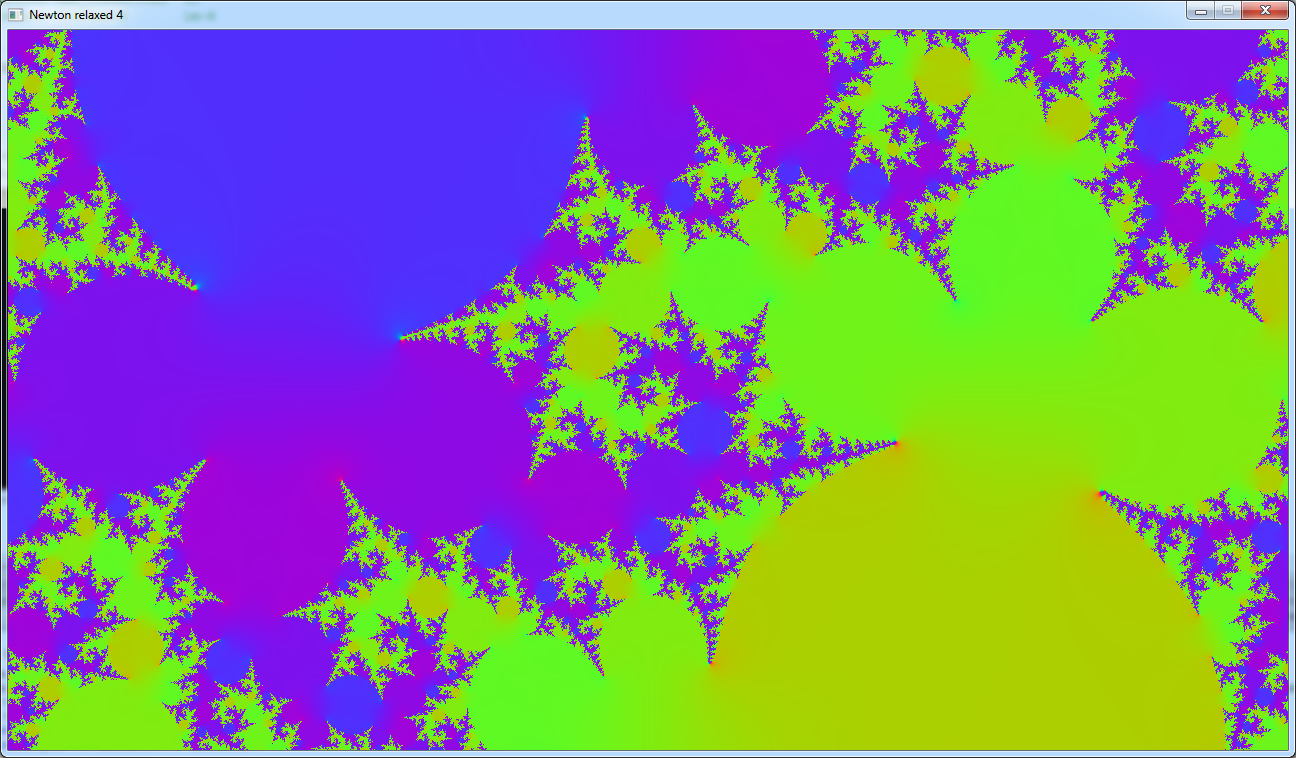
And here is an example with a = 1 and c = 0.3 + 0.3i
As the english wikipedia page explains there are 2 ways of computing a Nova fractal.
That's the same difference that we have between a Mandelbrot fractal and a Julia fractal.
For the first version of the Nova fractal we initialized "z" to the pixel's position and "c" stayed constant.
Now for this version c will be the pixel's position and we will initialize z to a constant value.
Here are the small modifications to the code:
// iterate
int iter;
Complex a(1, 0);
Complex c = z;
z = Complex(-1, 0);
for (iter = 0; iter < MAX_ITERATIONS; iter++)
{
Complex oldZ = z;
z = z - a * f(z) / df(z) + c;
Download source code
Download executable for Windows
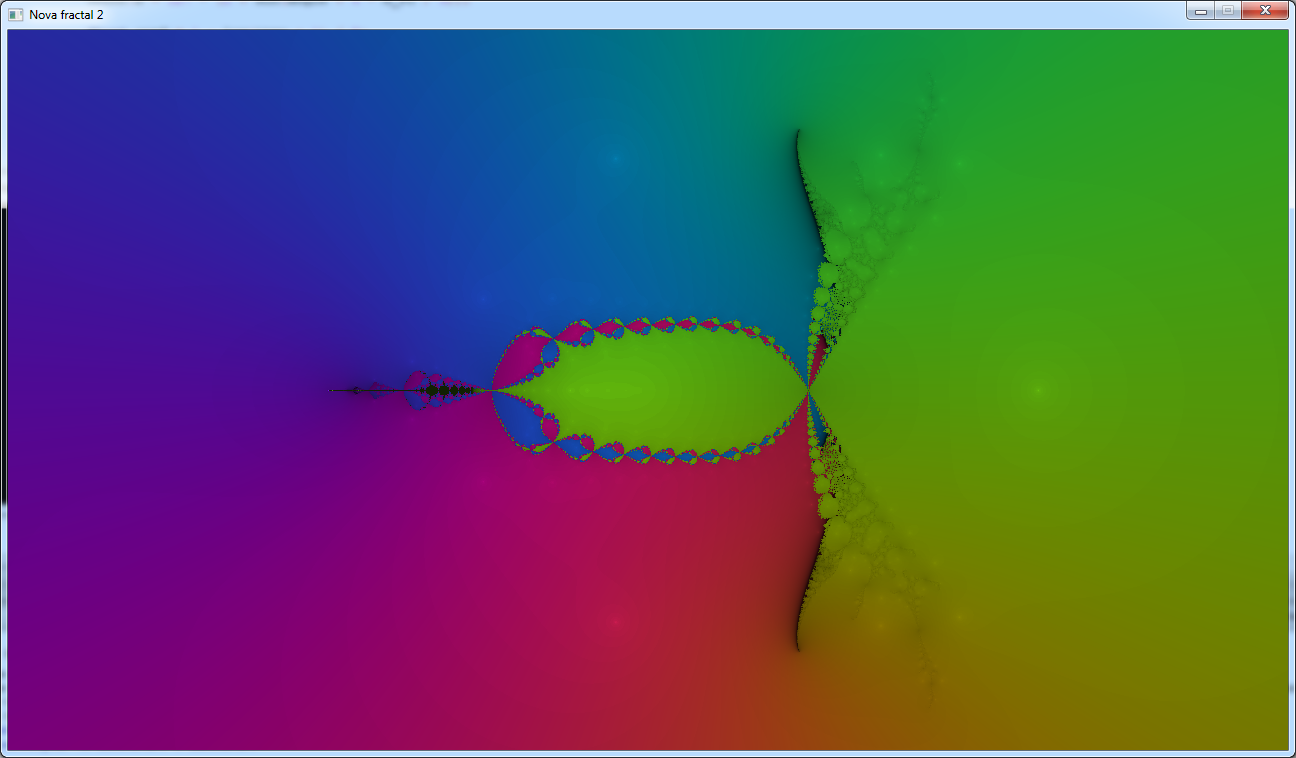
And this is what we get with a = 1 and z
0 = -1
That looks like some images I found
here.