The code in this article was written using Code::Blocks and SDL 2.
You can read
here a guide to install this software.
Although it is based on SDL, I don't use its functions directly. I have written a small library with a few basic
functions to ease the understanding and the portability to another language.
You can read more about this lib
here.
The idea for this article come from a
Numberphile video.
This video describes a mathematical object called sandpile.
The first part of the video defines some arithmetic operations on this object.
But at the end it shows a way to create fractal images that I will try to reproduce.
So let's see what a sandpile is and how it evolves.
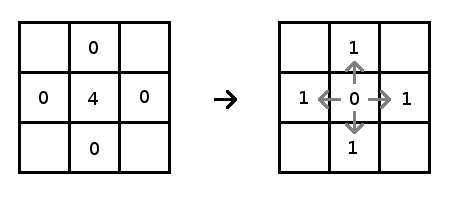
Consider a square grid. Each cell of this grid contains a number between 0 and 3.
If at any time one cell contains a value greater than 3, a topple rule occurs. The value of this cell is reduced
by 4, and the value of its 4 direct neighbours is increased by 1.
And this rule is repeated until there is no more cell with a value greater than 3.
To visualise the sandpiles we can assign a color to each cell depending on its value.
Now to produce a fractal, we simply need to use a grid large enough, to put a huge value in the center cell and to
repeat the topple rule as long as we can.
As the grid needs to be large enough, we will display one pixel per cell.
As the topple rule modifies the neighbour cells, internally we will store the grid as 2 integer arrays.
One will contain the current frame we are processing and the other will hold the previous frame.
This way we can apply the rule on every cell of one frame without bothering with side effects.
static int table[2][SCREEN_WIDTH][SCREEN_HEIGHT];
int currentTable = 0;
We initialize one of the arrays with full 0s except for the center cell which get a big value:
// initialise the table
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
table[currentTable][x][y] = 0;
table[currentTable][SCREEN_WIDTH / 2][SCREEN_HEIGHT / 2] = 400000;
To draw the cells we will need a palette that assigns a color to each possible cell value.
I tried to reproduce the palette that appears at 22:46 in the video:
- 0 is blue
- 1 is cyan
- 2 is yellow
- 3 is red
- and I added a white color for values greater than 3
// init palette
Color palette[5];
palette[0] = Color(0, 0, 255);
palette[1] = Color(0, 255, 255);
palette[2] = Color(255, 255, 0);
palette[3] = Color(255, 0, 0);
palette[4] = Color(255, 255, 255);
The drawing part is simple, we simply find the right color in the palette for each cell:
// draw the current table
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
int color = table[currentTable][x][y];
if (color > 4)
color = 4;
gfx.setPixel(x, y, palette[color]);
}
gfx.render();
sys.processEvents();
The update part is quite straigthforward too. First we copy the old grid to the current one.
// update the table
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
table[1 - currentTable][x][y] = table[currentTable][x][y];
}
Then we loop through each cell again to apply the topple rule if we find a value greater than 3.
Notice that we also check for each neighbour cell if it is not outside the grid.
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
if (table[currentTable][x][y] >= 4)
{
table[1 - currentTable][x][y] -= 4;
if (x - 1 >= 0)
table[1 - currentTable][x - 1][y] += 1;
if (x + 1 < SCREEN_WIDTH)
table[1 - currentTable][x + 1][y] += 1;
if (y - 1 >= 0)
table[1 - currentTable][x][y - 1] += 1;
if (y + 1 < SCREEN_HEIGHT)
table[1 - currentTable][x][y + 1] += 1;
}
}
Finally we switch the grids.
currentTable = 1 - currentTable;
Download source code
Download executable for Windows
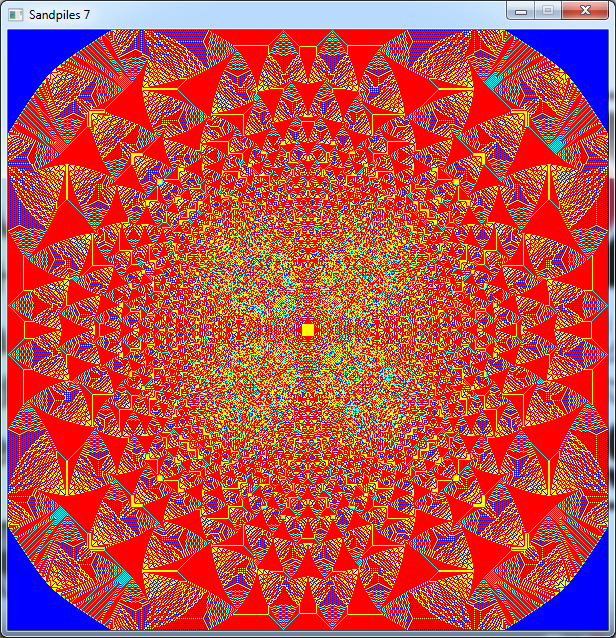
This is the result of ths program:
The only problem is that on my current PC with an i3-4330 this code take more that 30 minutes to complete.
So we will optimize that.
In our processing loop we have to check each neighbour cell to find if their are inside the grid.
These tests are expensive but there is an easy way to avoid them.
We will simply increase the size of the grid in all directions and we will only process and display the center.
static int table[2][SCREEN_WIDTH + 2][SCREEN_HEIGHT + 2];
[...]
for (int y = 1; y <= SCREEN_HEIGHT; ++y)
for (int x = 1; x <= SCREEN_WIDTH; ++x)
{
if (table[currentTable][x][y] >= 4)
{
table[1 - currentTable][x][y] -= 4;
table[1 - currentTable][x - 1][y] += 1;
table[1 - currentTable][x + 1][y] += 1;
table[1 - currentTable][x][y - 1] += 1;
table[1 - currentTable][x][y + 1] += 1;
}
}
And instead of writing a loop to copy the old grid into the current one before processing it, we can use the more
efficient memcpy function:
int screenSize = (SCREEN_WIDTH + 2) * (SCREEN_HEIGHT + 2);
memcpy(table[1 - currentTable], table[currentTable], screenSize * sizeof(int));
Download source code
Download executable for Windows
This code takes about 26 minutes and 40s on my computer.
That's faster but we can do better.
Redrawing the whole screen each frame is expensive because my lib is not particuarily optimized for the display.
And for this program we don't really want to see each step of the drawing. The most important thing is the final
picture.
We can easily modify the code to display the grid only every 16 process loops:
int counter = 0;
while (sys.isQuitRequested() == false)
{
[...]
counter++;
if ((counter % 16) == 0)
gfx.render();
Download source code
Download executable for Windows
This codes runs in about 18 minutes and 30s.
Now let's look at the operations of the topple rule.
If a cell is greater than or equal to 4, we substract 4 to it and spread 1 in each direction.
But if after substracting 4, if the value of the cell is still greater than or equal to 4, we'll have to wait the
next process loop to continue.
It would be more efficient if we repeat the rule until the value gets below 4.
Our process loop would look like this;
for (int y = 1; y <= SCREEN_HEIGHT; ++y)
for (int x = 1; x <= SCREEN_WIDTH; ++x)
{
while (table[currentTable][x][y] >= 4)
{
table[1 - currentTable][x][y] -= 4;
table[1 - currentTable][x - 1][y] += 1;
table[1 - currentTable][x + 1][y] += 1;
table[1 - currentTable][x][y - 1] += 1;
table[1 - currentTable][x][y + 1] += 1;
table[currentTable][x][y] -= 4;
}
}
Download source code
Download executable for Windows
Notice that we use the old grid's cell as a counter. We decrease it and we check it to get out of the loop.
This version takes only 2min and 35s to complete.
The program runs a lot faster now, but we can get further with a little trade-off.
First we can remove the while loop we introduced in the last part.
Indeed if we look at this loop, we decrease the cell value by 4 each time.
So we can predict how many times we will loop: that's the result of the initial value divided by 4.
And we can rewrite our processing loop like that:
for (int y = 1; y <= SCREEN_HEIGHT; ++y)
for (int x = 1; x <= SCREEN_WIDTH; ++x)
{
int height = table[currentTable][x][y] / 4;
table[1 - currentTable][x][y] -= 4 * height;
table[1 - currentTable][x - 1][y] += height;
table[1 - currentTable][x + 1][y] += height;
table[1 - currentTable][x][y - 1] += height;
table[1 - currentTable][x][y + 1] += height;
}
Now we saw that we use the old grid as a counter.
So we could probably use only one grid instead of 2.
That will avoid the memcpy operation.
There is always the danger of having a side effect when you do this kind of things, as the topple rule will modify
the next cell we will process.
But this rule is simple and even if the operations are not in the same order, everything will be solved with the
following loops.
The main trade-off of using only one grid is that when the program is running, it will not look symetrical.
So here is the full code when we use only one grid:
#include <stdio.h>
#include <stdlib.h>
#include "main.h"
#include "Graphics.h"
#include "System.h"
#define SCREEN_WIDTH 600
#define SCREEN_HEIGHT 600
int main(int argc, char* argv[])
{
// init the window
gfx.init("Sandpiles 5", SCREEN_WIDTH, SCREEN_HEIGHT);
gfx.init2D();
gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));
static int table[SCREEN_WIDTH + 2][SCREEN_HEIGHT + 2];
// initialise the table
for (int y = 1; y <= SCREEN_HEIGHT; ++y)
for (int x = 1; x <= SCREEN_WIDTH; ++x)
table[x][y] = 0;
table[SCREEN_WIDTH / 2][SCREEN_HEIGHT / 2] = 400000;
// init palette
Color palette[5];
palette[0] = Color(0, 0, 255);
palette[1] = Color(0, 255, 255);
palette[2] = Color(255, 255, 0);
palette[3] = Color(255, 0, 0);
palette[4] = Color(255, 255, 255);
int counter = 0;
while (sys.isQuitRequested() == false)
{
// draw the current table
for (int y = 0; y < SCREEN_HEIGHT; ++y)
for (int x = 0; x < SCREEN_WIDTH; ++x)
{
int color = table[x + 1][y + 1];
if (color > 4)
color = 4;
gfx.setPixel(x, y, palette[color]);
}
counter++;
if ((counter % 16) == 0)
gfx.render();
sys.processEvents();
// update the table
int screenSize = (SCREEN_WIDTH + 2) * (SCREEN_HEIGHT + 2);
for (int y = 1; y <= SCREEN_HEIGHT; ++y)
for (int x = 1; x <= SCREEN_WIDTH; ++x)
{
int height = table[x][y] / 4;
table[x][y] -= height * 4;
table[x - 1][y] += height;
table[x + 1][y] += height;
table[x][y - 1] += height;
table[x][y + 1] += height;
}
}
gfx.quit();
return EXIT_SUCCESS;
}
Download source code
Download executable for Windows
And this program takes only 1min 33s to draw the final image. That's 20 times faster than the first one.
And of course the image we get is the same as the first one.
Now that we have a fast way to display our fractal, we can try to play with it to see if we can change its shape.
First let's see what happens if we start with 3 cells that have a high value instead of one.
Will they collide with each others and change the shape of the final fractal ?
To do this we only have to change the initialization part of our program:
int cx = SCREEN_WIDTH / 2 + 1;
int cy = SCREEN_HEIGHT / 2 + 1;
table[cx][cy-70] = 200000;
table[cx-50][cy+50] = 150000;
table[cx+50][cy+50] = 150000;
Download source code
Download executable for Windows
Here is a picture of what we see at the beginning of the execution:
And this is what we get at the end.
Although the central chaotic part does not have the same shape, the outer "ordered" ring doesn't look very
different.
What will happen if we try to draw a square at the beginning instead of using a few points ?
If we modify the initialization like that:
int cx = SCREEN_WIDTH / 2 + 1;
int cy = SCREEN_HEIGHT / 2 + 1;
for (int i = -50; i <= 49; ++i)
{
table[cx - 50][cy + i] = 2500;
table[cx + 49][cy + i] = 2500;
table[cx + i][cy - 50] = 2500;
table[cx + i][cy + 49] = 2500;
}
Download source code
Download executable for Windows
This is what we see at the beginning:
And what we get at the end.
Again the shape doesn't look very different.
Instead of starting with an empty grid, let's try to fill half of it with "1" cells.
// initialise the table
for (int y = 1; y <= SCREEN_HEIGHT; ++y)
for (int x = 1; x <= SCREEN_WIDTH; ++x)
table[x][y] = (y > x ? 1 : 0);
int cx = SCREEN_WIDTH / 2;
int cy = SCREEN_HEIGHT / 2;
table[cx][cy] = 400000;
Download source code
Download executable for Windows
This is what we get:
Now it's interesting. The lower part looks stretched as if we looked at it through a magnifying glass.
You can also notice that its shape is not very circular. It looks more like an octagon.
Now what do we get if the half grid is not filled with plain 1's, but with a pattern instead?
Let's try to initialize it with a checkerboard pattern of 1s and 2s cells.
// initialise the table
for (int y = 1; y <= SCREEN_HEIGHT; ++y)
for (int x = 1; x <= SCREEN_WIDTH; ++x)
table[x][y] = (y > x ? (((y+x)&1) ? 2 : 1) : 0);
int cx = SCREEN_WIDTH / 2 + 1;
int cy = SCREEN_HEIGHT / 2 + 1;
table[cx][cy] = 400000;
Download source code
Download executable for Windows
Here is the final image:
The pattern seems to have "survived" the operation, and the triangles we get seem to be filled with new types of
patterns.
The original video also showed images made with other rules. For example they allowed cells to contain values
greater than 3.
It should not be difficult to modifiy this code according to these new rules.
I hope you'll have fun exploring this world of cool fractals.






 Original video from Numberphile
Original video from Numberphile