Reaction-Diffusion (2)

Mitosis

In the last article we saw how to code a reaction-diffusion and optimised it the best we could.
Now we will try different values for f and k and see what happens.

In this article we will initialize the tables with several squares of B instead of only one:

		for (int i = 0; i < 10; i++)
		{
			int sze = 10 + (rand() % 10);
			int px = sze + (rand() % (SCREEN_WIDTH  - sze * 2));
			int py = sze + (rand() % (SCREEN_HEIGHT - sze * 2));

			for (int y = 0; y < sze; ++y)
				for (int x = 0; x < sze; ++x)
					table[0][1][px + x][py + y] = 1.0;
		}

Now let's try these coefficients:

		double f = 0.038;
		double k = 0.065;

		Download source code
		Download executable for Windows

We can see small spots duplicating themselves until they fill the whole screen.

Clovers

With these parameters:

		double f = 0.042;
		double k = 0.061;

		Download source code
		Download executable for Windows

This one looks a bit like the programs of the previous article.
Clovers spread getting more and more complex until they meet each other, creating a maze like pattern.

Rings

With these parameters:

		double f = 0.062;
		double k = 0.063;

		Download source code
		Download executable for Windows

Circles grow, slowly getting more like clovers. When they can't get more complex, worms spread from their ends
At the end we get a maze like image like in the last article.

Unstable

For this one we will need a few more starting squares and they will have less concentration

		for (int i = 0; i < 15; i++)
		{
			[...]

			for (int y = 0; y < sze; ++y)
				for (int x = 0; x < sze; ++x)
					table[0][1][px + x][py + y] = 0.6;
		}

Now we will use a low value for f

		double f = 0.01;
		double k = 0.045;

		Download source code
		Download executable for Windows

This one is interesting. Circles will grows quickly. Reappearing cyclically.
Until we get to a state where they appear continually.
The result is not guaranteed. If you are unlucky the reaction will stop and you will get a screen completely red.
But it works 70% of the time.

This beahviour is similar to the Belousov-Zhabotinsky chemical reaction. See the links section for a video.

Mapping the parameters

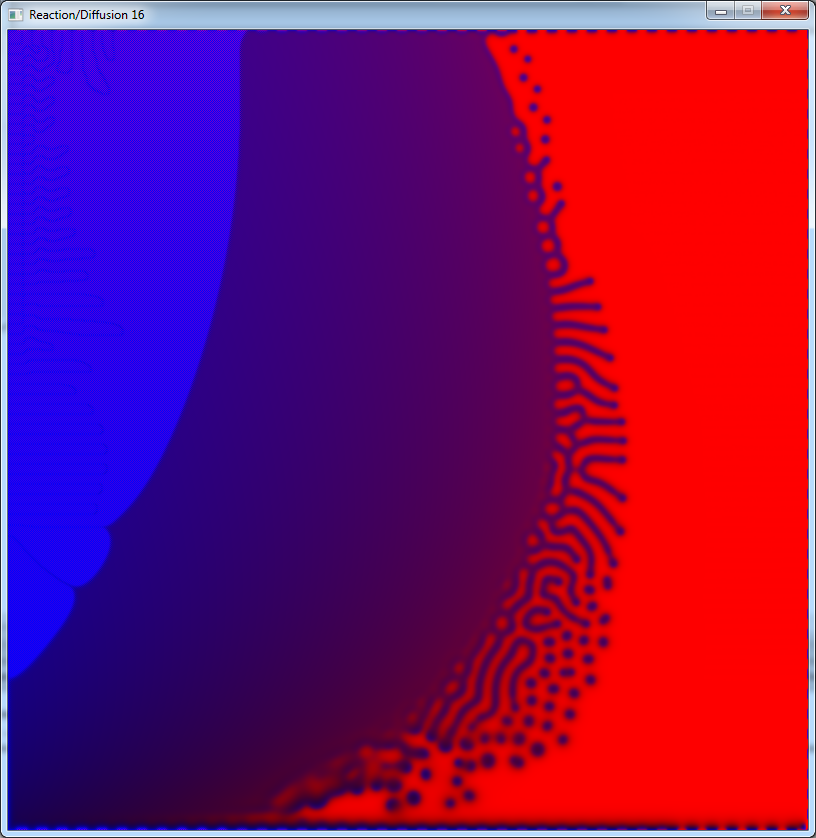
Now let's try to produce an image where we can see all these behaviours together.
We always used a constant value for the f and k. Now we will try to give them a value depending on the
coordinates on the screen.

First we will draw a bigger image this time:

		#define SCREEN_WIDTH    800
		#define SCREEN_HEIGHT   800

We will initialize the tables as a checkerboard of A and B.

		//  initialize the table
		for (int y = 0; y < SCREEN_HEIGHT+2; ++y)
			for (int x = 0; x < SCREEN_WIDTH+2; ++x)
				for (int t = 0; t < 2; ++t)
				{
					int check = ((x / 10) % 2) ^ ((y / 10) % 2);
					table[t][0][y][x] = check;
					table[t][1][y][x] = 1 - check;
				}

The f and k will be computed inside the loops of update():

		for (int y = 1; y < SCREEN_HEIGHT+1; ++y)
			for (int x = 1; x < SCREEN_WIDTH+1; ++x)
			{
				double f = 0.01 + 0.09 * (SCREEN_HEIGHT - y) / (SCREEN_HEIGHT - 1);
				double k = 0.02 + 0.06 * (x - 1) / (SCREEN_WIDTH - 1);
				double ca = 1.0 - f - 1.8 * DA;
				double cb = 1.0 - f - 1.8 * DB - k;

Due to the the great range of values f and k can take, the concentrations could get bigger than 1.
So we need to check that in update too.

		for (int t = 0; t < 2; ++t)
		{
			if (table[1-curT][t][y][x] < 0.0)
				table[1-curT][t][y][x] = 0.0;
			if (table[1-curT][t][y][x] > 1.0)
				table[1-curT][t][y][x] = 1.0;
		}

Finally at the beginning of update we will fill the leftmost column with B and the rightmost with A to avoid black
lines appearing at the borders of the screen.

		for (int t = 0; t < 2; ++t)
		{
			for (int y = 0; y < SCREEN_HEIGHT + 2; ++y)
			{
				table[curT][t][y][SCREEN_WIDTH - 1] = (t == 0 ? 1.0 : 0.0);
				table[curT][t][y][0] = (t == 0 ? 0.0 : 1);
				table[1-curT][t][y][SCREEN_WIDTH - 1] = (t == 0 ? 1.0 : 0.0);
				table[1-curT][t][y][0] = (t == 0 ? 0.0 : 1);
			}
		}

		Download source code
		Download executable for Windows

And after a few seconds we can see that:

You will find a much more detailed version of this image in a link below.