The Lissajous curves

About the code

The code in this article was written using Code::Blocks and SDL 2.
You can read here a guide to install this sofware.
Although it is based on SDL, I don't use its functions directly. I have written a small library with a few basic
functions to ease the understanding and the portability to another language.
You can read more about this lib here.

This article uses the line function we added in the Bresenham's line algorithm.

Playing again with the circle

In a previous article we talked about the circle and found these equations

		x = x_C + R * cos θ
		y = y_C + R * sin θ

We tried to change the radii and to add a value to the angle θ and we got various ellipses.
But what happens if we multiply θ by a value ?

		x = x_C + R * cos(a₁ * θ)
		y = y_C + R * sin(a₂ * θ)

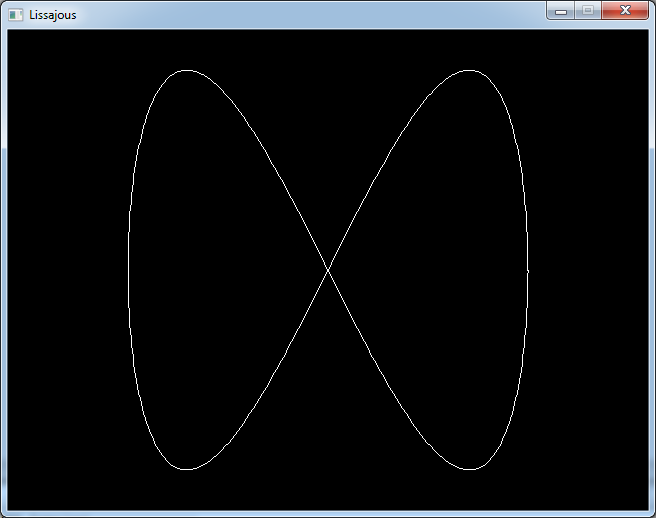
Let's try with a₁ = 1 and a₂ = 2;

		int main(int argc, char* argv[])
		{
			// init the window
			gfx.init("Lissajous", SCREEN_WIDTH, SCREEN_HEIGHT);
			gfx.init2D();
			gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));

			int centerX = SCREEN_WIDTH / 2;
			int centerY = SCREEN_HEIGHT / 2;
			int radius = 200;

			for (int i = 0; i < 360; i++)
			{
				float angle0 = DEG_TO_RAD(i);
				int x0 = centerX + radius * cos(angle0);
				int y0 = centerY + radius * sin(2.0 * angle0);

				float angle1 = DEG_TO_RAD(i + 1);
				int x1 = centerX + radius * cos(angle1);
				int y1 = centerY + radius * sin(2.0 * angle1);

				gfx.line(x0, y0, x1, y1, Color(255, 255, 255));

				gfx.render();
				sys.wait(20);
			}

			// wait until we quit
			while (sys.isQuitRequested() == false)
			{
				gfx.render();
				sys.wait(20);
				sys.processEvents();
			}

			gfx.quit();

			return EXIT_SUCCESS;
		}

		Download source code
		Download executable for Windows

We get a curve that looks like an infinity symbol.

A family of curves

If we vary a₁ and a₂ between 1 and 5 we get different shapes.

		#define SCREEN_WIDTH    640
		#define SCREEN_HEIGHT   640

		int main(int argc, char* argv[])
		{
			// init the window
			gfx.init("Lissajous 2", SCREEN_WIDTH, SCREEN_HEIGHT);
			gfx.init2D();
			gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));


			for (int i = 0; i < 360; i++)
			{
				for (int c2 = 1; c2 < 6; c2++)
					for (int c1 = 1; c1 < 6; c1++)
					{
						int centerX = SCREEN_WIDTH / 2 + (c1 - 3) * 120;
						int centerY = SCREEN_HEIGHT/ 2 + (c2 - 3) * 120;
						int radius = 50;

						float angle0 = DEG_TO_RAD(i);
						int x0 = centerX + radius * cos(c1 * angle0);
						int y0 = centerY + radius * sin(c2 * angle0);

						float angle1 = DEG_TO_RAD(i + 1);
						int x1 = centerX + radius * cos(c1 * angle1);
						int y1 = centerY + radius * sin(c2 * angle1);

						gfx.line(x0, y0, x1, y1, Color(255, 255, 255));
					}

				gfx.render();
				sys.wait(20);
			}

			// wait until we quit
			while (sys.isQuitRequested() == false)
			{
				gfx.render();
				sys.wait(20);
				sys.processEvents();
			}

			gfx.quit();

			return EXIT_SUCCESS;
		}

		Download source code
		Download executable for Windows

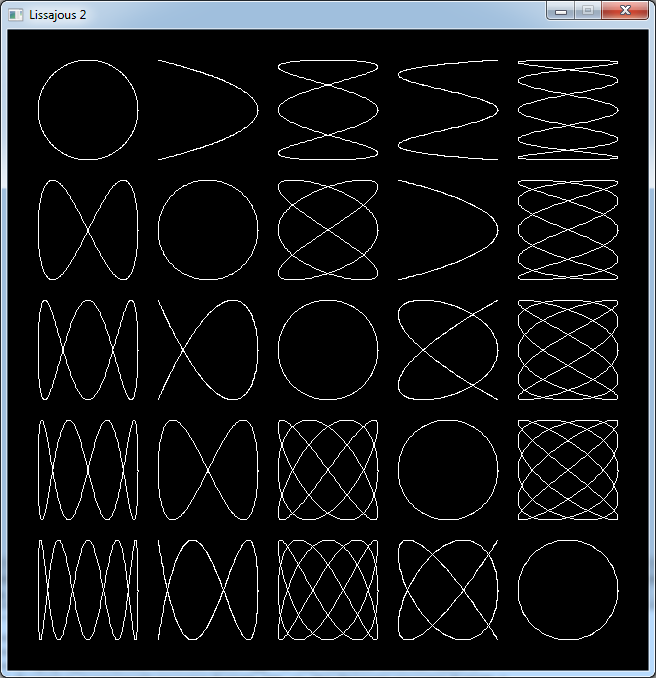
These shapes are called Lissajous curves.
Well in fact it is not the real definition of a Lissajous as it should use 2 sines:

		x = x_C + R * sin(a₁ * θ)
		y = y_C + R * sin(a₂ * θ)

But our definition gives the same kind of curves.

In electronics when you use an oscilloscope, you can plug in a sine current to deflect the spot horizontally and
another one to deflect it vertically.
If the currents have different frequencies you will then see this kind of curves.
This is a method used to measure the phase difference between the two currents.

This curve also represents the movement of a double-pendulum, where one pendulum moves along the x axis and the
other moves along the y axis.

Now we only used integers for a₁ and a₂.
You can also try with non integer values. You will then need to change the angle further than 360 degrees to get
the full curve.
But you will get the same kind of shapes because it's only the a₁ / a₂ that defines them.

Filling the curve

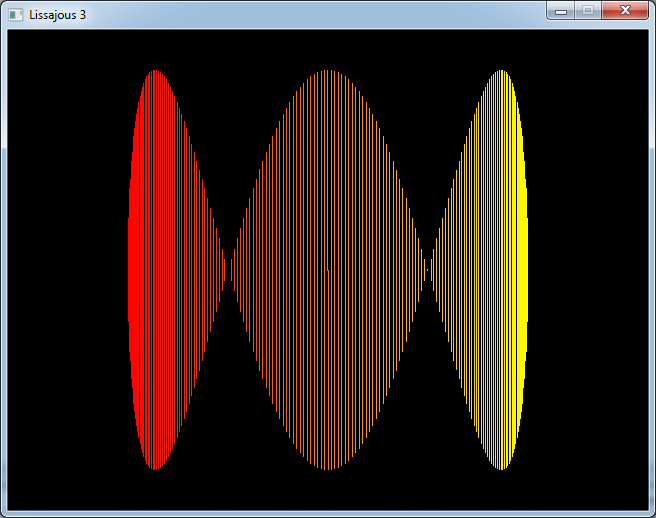
As many of these curve are symmetrical with respect to the x axis, one way to get a filled shape is to draw
vertical lines from this axis.

		int main(int argc, char* argv[])
		{
			// init the window
			gfx.init("Lissajous 3", SCREEN_WIDTH, SCREEN_HEIGHT);
			gfx.init2D();
			gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));

			int centerX = SCREEN_WIDTH / 2;
			int centerY = SCREEN_HEIGHT/ 2;
			int radius = 200;

			for (int i = 0; i < 360; i++)
			{
				float angle = DEG_TO_RAD(i);
				int x = centerX + radius * cos(angle);
				int y = centerY + radius * sin(3.0 * angle);

				Color c;
				c.r = 255;
				c.g = 128 + 127 * cos(angle);
				c.b = 0;
				gfx.line(x, y, x, centerY, c);

				gfx.render();
				sys.wait(20);
			}

			// wait until we quit
			while (sys.isQuitRequested() == false)
			{
				gfx.render();
				sys.wait(20);
				sys.processEvents();
			}

			gfx.quit();

			return EXIT_SUCCESS;
		}

		Download source code
		Download executable for Windows

Multiplication and addition

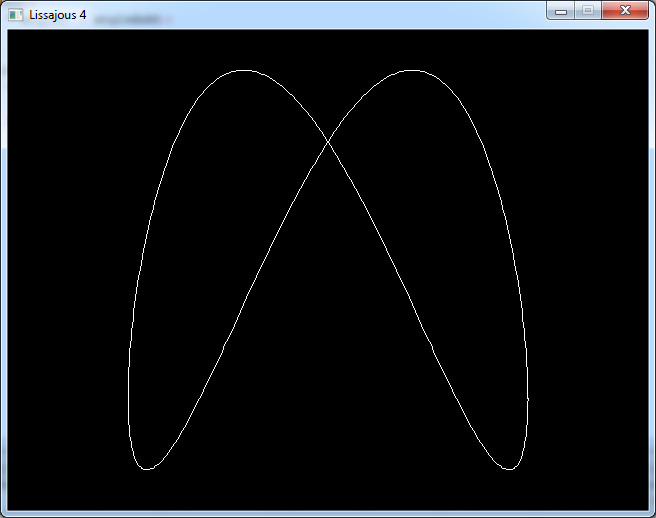
Now what happens if we add a value to the angle like we did in the last article ?

		float angleAdd = DEG_TO_RAD(40);

		for (int i = 0; i < 360; i++)
		{
			float angle0 = DEG_TO_RAD(i);
			int x0 = centerX + radius * cos(angle0);
			int y0 = centerY + radius * sin(2.0 * angle0 + angleAdd);

			float angle1 = DEG_TO_RAD(i + 1);
			int x1 = centerX + radius * cos(angle1);
			int y1 = centerY + radius * sin(2.0 * angle1 + angleAdd);

			gfx.line(x0, y0, x1, y1, Color(255, 255, 255));

			gfx.render();
			sys.wait(20);
		}

		Download source code
		Download executable for Windows

We get a distorted curve