The Voronoi diagram

Definition

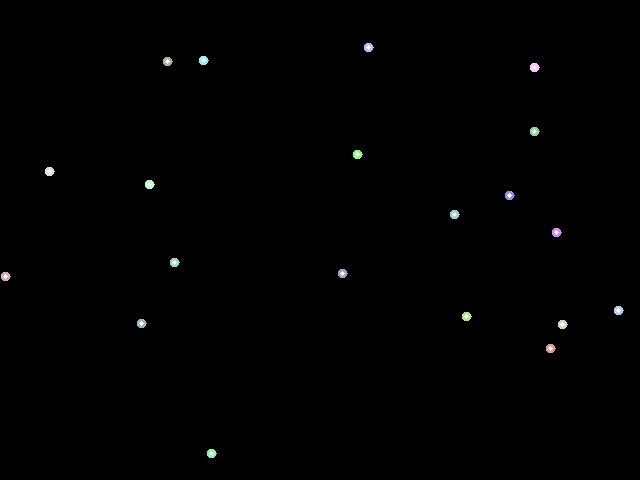
Let's take a bunch of points on the screen that we'll call "seeds".

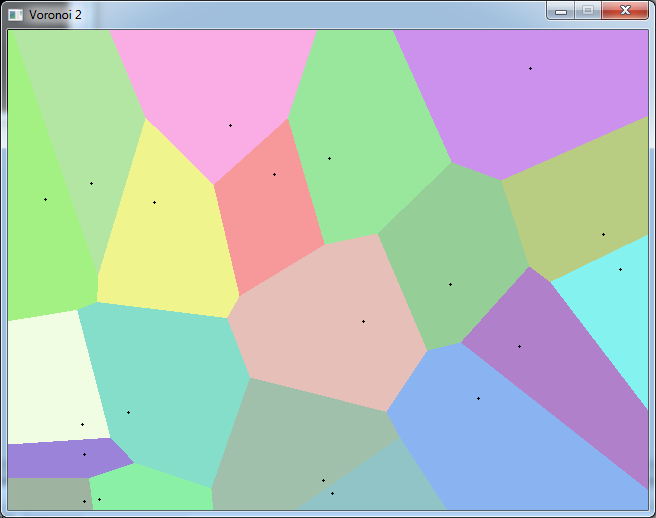
The Voronoi diagram looks like this:

It divides the screen into cells.
Each cell contains only one "seed", and each point in this cell is nearest from this seed than from any other one.

This diagram is used in many fields. In example:

It can be used in A.I. to find a path from one point to the nearest seed.
It can represent the crystal structure of a material.
In telephony, when your cell phone is connected to the nearest antenna you are inside of its cell.
In computer graphics it can be used to draw the patches on a giraffe.

There are many algorithms to build this diagram here I will use one of the most visual and easiest to compute.

Easy algorithm

The idea is to draw circles around each of our seeds and to make them grow all at the same pace until they touch
another circle.
That's to say when we want to draw a pixel of our circle we will only do it if the current color of this pixel is
black. If it's not the case then we have met another circle.

But first, we will initialise our seeds and choose a color for each one of them.

		#define SCREEN_WIDTH    640
		#define SCREEN_HEIGHT   480
		#define NB_POINTS 20

		struct SPoint
		{
			int     x, y;
			Color   col;
		};

		int main(int argc, char* argv[])
		{
			SPoint  points[NB_POINTS];
			float radius = 1.0;

			// init the window
			gfx.init("Voronoi", SCREEN_WIDTH, SCREEN_HEIGHT);
			gfx.init2D();
			gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));

			// init the points
			srand(time(NULL));

			for (int i = 0; i < NB_POINTS; ++i)
			{
				points[i].x = rand() % SCREEN_WIDTH;
				points[i].y = rand() % SCREEN_HEIGHT;
				points[i].col = Color((rand() % 128) + 128,
				                      (rand() % 128) + 128,
				                      (rand() % 128) + 128);
			}

Then for each point we will draw the circle. If you don't understand the formulas used to draw the circle, they are
explained here.

			while (sys.isQuitRequested() == false)
			{
				sys.processEvents();

				// drawing
				for (int i = 0; i < NB_POINTS; ++i)
				{
					// draw circles
					for (float a = 0.0; a < 2.0 * M_PI; a += M_PI / 1500.0)
					{
						int x = points[i].x + (int)(radius * cos(a));
						int y = points[i].y + (int)(radius * sin(a));

						// if pixel is not out of screen
						if (x >= 0 && x < SCREEN_WIDTH &&
						    y >= 0 && y < SCREEN_HEIGHT)
						{
							// if pixel is empty
							if (gfx.getPixel(x, y).argb == Color(0, 0, 0, SDL_ALPHA_OPAQUE).argb)
								gfx.setPixel(x, y, points[i].col);
						}
					}

Finally we draw the points over the circles, increase the radius and loop back.

					// draw points
					gfx.setPixel(points[i].x    , points[i].y    , Color(1, 1, 1, SDL_ALPHA_OPAQUE));
					gfx.setPixel(points[i].x    , points[i].y - 1, Color(1, 1, 1, SDL_ALPHA_OPAQUE));
					gfx.setPixel(points[i].x    , points[i].y + 1, Color(1, 1, 1, SDL_ALPHA_OPAQUE));
					gfx.setPixel(points[i].x - 1, points[i].y    , Color(1, 1, 1, SDL_ALPHA_OPAQUE));
					gfx.setPixel(points[i].x + 1, points[i].y    , Color(1, 1, 1, SDL_ALPHA_OPAQUE));
				}

				// increase radius
				radius += 1.0;

				gfx.render();
				sys.wait(50);
			}

		Download source code
		Download executable for Windows

The result looks like the image we saw before.
But it's not always perfect if 2 points are very close:

That comes from small rounding errors in the circle drawing, and from the fact that we do not draw the all circles
at the same time, but one after the other.

Thinking the other way

To fix that, we will do something that we will often do in the future: we will revert the problem.

Let's think about the result.
What do we want to get ? The color of each pixel of the screen.
So we will first loop over all the pixels of the screen:

        for (int y = 0; y < SCREEN_HEIGHT; ++y)
            for (int x = 0; x < SCREEN_WIDTH; ++x)
            {

Now if we follow the definition we gave at the beginning this pixel is inside the cell of one seed.
All the points in a cell are nearer from its seed than from all the other seeds.
So if we found the closest seed to this pixel, we know that it is inside its cell and should get its color.

So we will loop over all the points, compute its distance from our pixel, and keep the nearest one.

                int     nearest = 0;
                Sint32  nearestDist = 1000000000;

                for (int i = 0; i < NB_POINTS; ++i)
                {
                    Sint32  dx = points[i].x - x;
                    Sint32  dy = points[i].y - y;
                    Sint32  dist = dx * dx + dy * dy;

                    if (dist < nearestDist)
                    {
                        nearest = i;
                        nearestDist = dist;
                    }
                }

Now we only have to draw the pixel with the color of the nearest point.
With this method we could draw all the pixels of the screen in one pass.
But as I want to keep the animation effect of the growing circles, I will only draw the pixel if the distance is
less than the current radius.

                if (sqrt(nearestDist) <= radius)
                    gfx.setPixel(x, y, points[nearest].col);

		Download source code
		Download executable for Windows

With this program, now the lines are perfectly straight.