The code in this article was written using Code::Blocks and SDL 2.
You can read
here a guide to install this software.
Although it is based on SDL, I don't use its functions directly. I have written a small library with a few basic
functions to ease the understanding and the portability to another language.
You can read more about this lib
here.
In this article I use the vector class I first talked about
here.
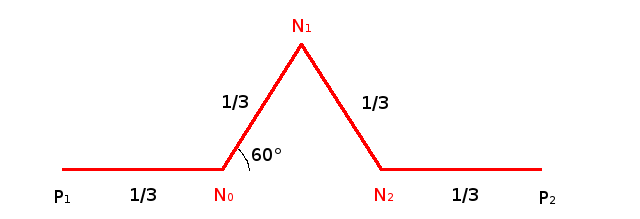
The von Koch curve is one of the simplest fractals often used as an example to teach what a fractal is.
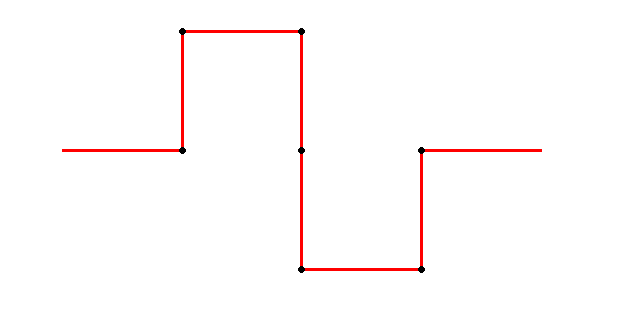
Here is the definition of its first step. First we start with a line that we suppose of length 1 for simplicity.
We divide this segments in 3 equal parts:
We remove the middle one.
And we draw 2 more segments an 60° angle so that the center part looks like an equilateral triangle without the
bottom.
Then we repeat this process for each of these 4 segments. We repeat it for each new segment we created.
And so on.
So to code that we will write a vonKoch function that will take start and end points of the line, along with a
level variable that we will explain later.
void vonKoch(Vec2f p1, Vec2f p2, int level)
{
We will compute the positions of the N
0, N
1 and N
2 point as we described above.
Vec2f n[3];
Vec2f v12 = p2 - p1;
n[0] = p1 + v12 * 1 / 3;
n[2] = p1 + v12 * 2 / 3;
Vec2f v02 = n[2] - n[0];
v02.rotate(DEG_TO_RAD(-60));
n[1] = n[0] + v02;
And then we will call the function again for each segment we have
vonKoch( p1, n[0], level + 1);
vonKoch(n[0], n[1], level + 1);
vonKoch(n[1], n[2], level + 1);
vonKoch(n[2], p2, level + 1);
}
But if we run this program like that it will never exit this function.
We need a way to get out of it after a given number of iterations.
So at the beginning of the function we will test the level variable which is in fact a simple counter.
int maxLevel = 5;
void vonKoch(Vec2f p1, Vec2f p2, int level)
{
if (level >= maxLevel)
{
And as we are here at the maximum level we will draw the line on the screen and exit the function.
gfx.line(p1.x, p1.y, p2.x, p2.y, Color(255, 255, 255));
return;
}
Then in the main function we will simply call the vonKoch function with the coordinates of our starting line.
Vec2f left ( 0, SCREEN_HEIGHT/2);
Vec2f right(SCREEN_WIDTH-1, SCREEN_HEIGHT/2);
vonKoch(left, right, 0);
Download source code
Download executable for Windows
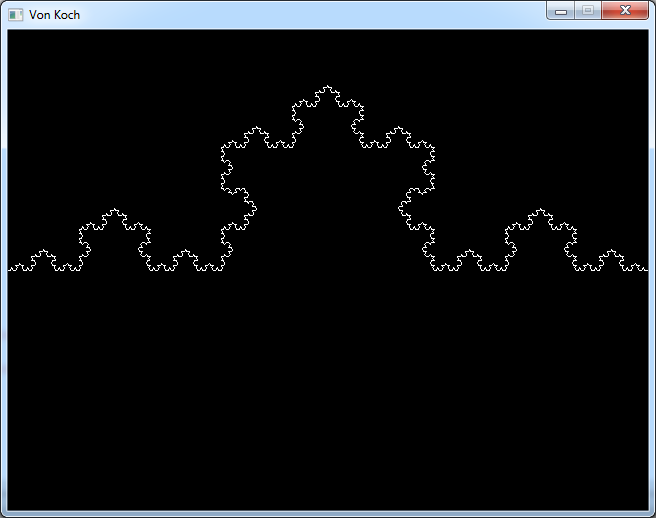
And this is the result of this program:
The simplest way to animate this program is to render the screen and wait a little bit right after we draw the
line.
As the calls to vonKoch() are ordered, we will see the curve drawing from the left to the right.
if (level >= maxLevel)
{
gfx.line(p1.x, p1.y, p2.x, p2.y, Color(255, 255, 255));
gfx.render();
sys.wait(20);
return;
}
Download source code
Download executable for Windows
But there is a better way to animate it by displaying the successives steps of the fractal.
To do that, we have to call the display routine inside the main loop.
int cnt = 0;
// wait until we quit
while (sys.isQuitRequested() == false)
{
if (cnt == 0)
{
gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));
vonKoch(left, right, 0);
}
The cnt variable is a counter that will be increased. And each time it will get to 50, we will increase the
maxLevel variable until it reaches a maximum value.
cnt++;
if (maxLevel < 6 && cnt == 50)
{
cnt = 0;
maxLevel++;
}
As we wait for 20 ms in each main loop, maxLevel will be increased every 50 * 20 ms, so every second.
gfx.render();
sys.wait(20);
sys.processEvents();
}
Download source code
Download executable for Windows
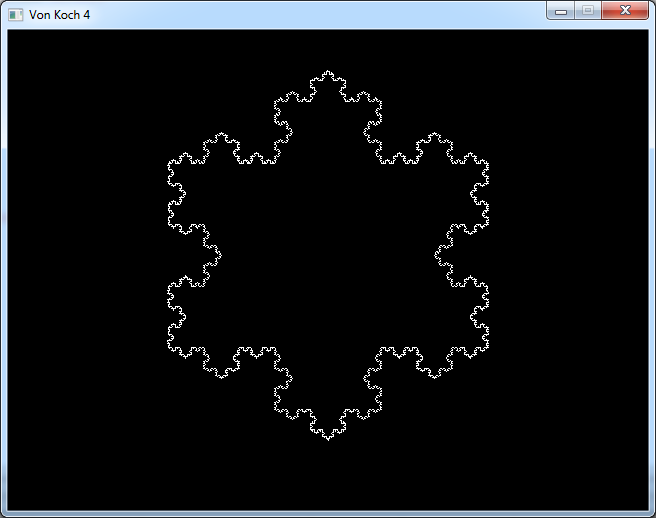
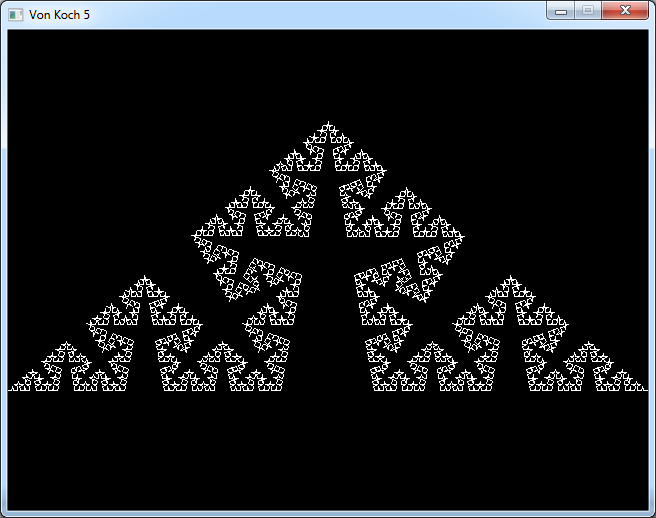
The von Koch snowflake uses the same process as the von Koch curve.
But now we start with a triangle instead of a single line.
Vec2f left (SCREEN_WIDTH/2 - SCREEN_WIDTH/4, (SCREEN_HEIGHT*5)/18);
Vec2f right(SCREEN_WIDTH/2 + SCREEN_WIDTH/4, (SCREEN_HEIGHT*5)/18);
Vec2f v = right - left;
v.rotate(DEG_TO_RAD(60));
Vec2f bottom = left + v;
Then we will call the draw function 3 times. One time for each line.
if (cnt == 0)
{
gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));
vonKoch(left, right, 0);
vonKoch(right, bottom, 0);
vonKoch(bottom, left, 0);
}
Download source code
Download executable for Windows
And here is the result after 5 steps:
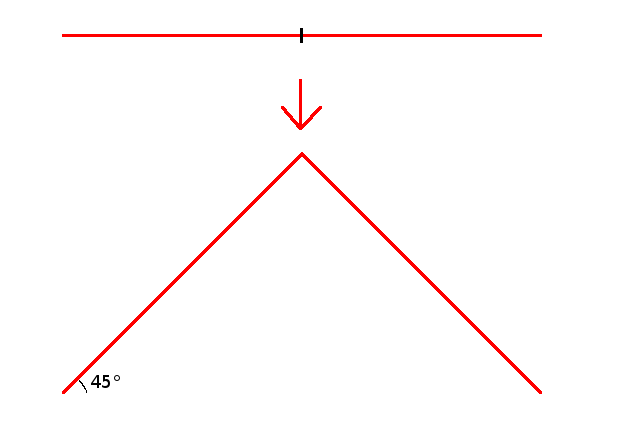
The Cesàro fractal is a more spiky version of the von Koch curve.
The construction is the same but the angle of central segments is greater than 60°.
To program that it I chose a 80° angle:
Vec2f n[3];
Vec2f v12 = p2 - p1;
n[0] = p1 + v12 * 0.427f;
n[2] = p2 - v12 * 0.427f;
Vec2f v = n[0] - p1;
v.rotate(DEG_TO_RAD(-80));
n[1] = n[0] + v;
vonKoch( p1, n[0], level + 1);
vonKoch(n[0], n[1], level + 1);
vonKoch(n[1], n[2], level + 1);
vonKoch(n[2], p2, level + 1);
Download source code
Download executable for Windows
And here is what it looks like:
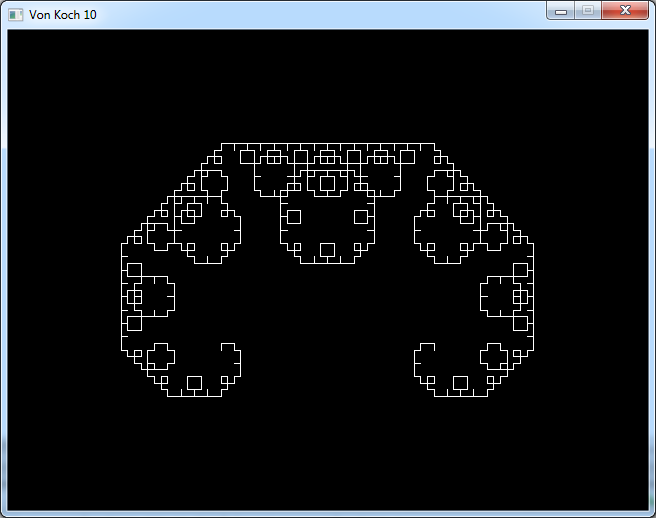
The quadratic von Koch rule is as follow:
Vec2f n[7];
Vec2f v = (p2 - p1) / 4;
Vec2f v2 = v;
v2.rotate(DEG_TO_RAD(-90));
n[0] = p1 + v;
n[6] = p2 - v;
n[1] = n[0] + v2;
n[5] = n[6] - v2;
n[2] = n[1] + v;
n[4] = n[5] - v;
n[3] = (n[2] + n[4]) / 2;
vonKoch( p1, n[0], level + 1);
vonKoch(n[0], n[1], level + 1);
vonKoch(n[1], n[2], level + 1);
vonKoch(n[2], n[3], level + 1);
vonKoch(n[3], n[4], level + 1);
vonKoch(n[4], n[5], level + 1);
vonKoch(n[5], n[6], level + 1);
vonKoch(n[6], p2, level + 1);
Download source code
Download executable for Windows
This is what we get after 4 iterations:
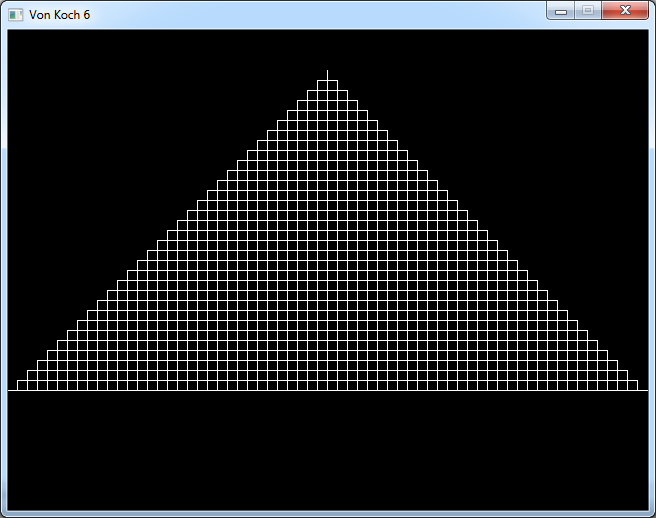
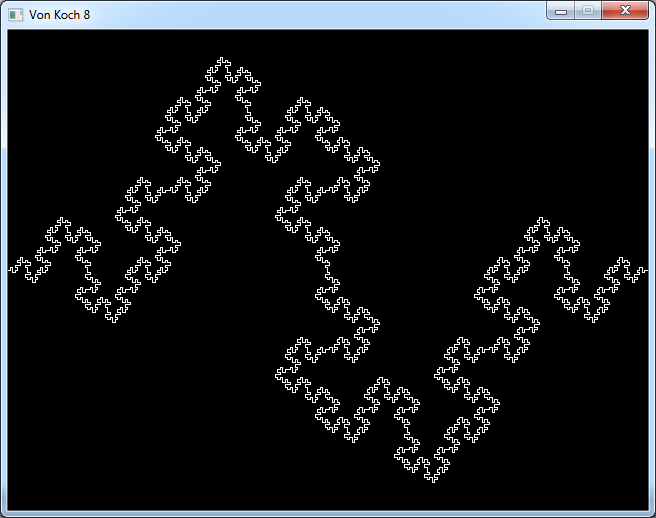
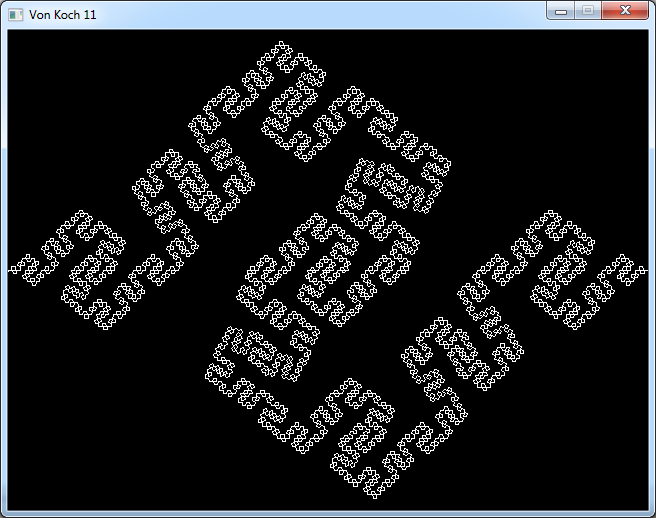
If we apply the quadratic rule on a square we get what is called a quadratic island, or quadratic flake.
Vec2f p[4];
p[0] = Vec2f(SCREEN_WIDTH/2 - SCREEN_HEIGHT/4, SCREEN_HEIGHT /4);
p[1] = Vec2f(SCREEN_WIDTH/2 + SCREEN_HEIGHT/4, SCREEN_HEIGHT /4);
p[3] = Vec2f(SCREEN_WIDTH/2 - SCREEN_HEIGHT/4, (SCREEN_HEIGHT*3)/4);
p[2] = Vec2f(SCREEN_WIDTH/2 + SCREEN_HEIGHT/4, (SCREEN_HEIGHT*3)/4);
[...]
for (int i = 0; i < 4; i++)
{
int n = (i + 1) %4;
vonKoch(p[i], p[n], 0);
}
Download source code
Download executable for Windows
And this is what it looks like:
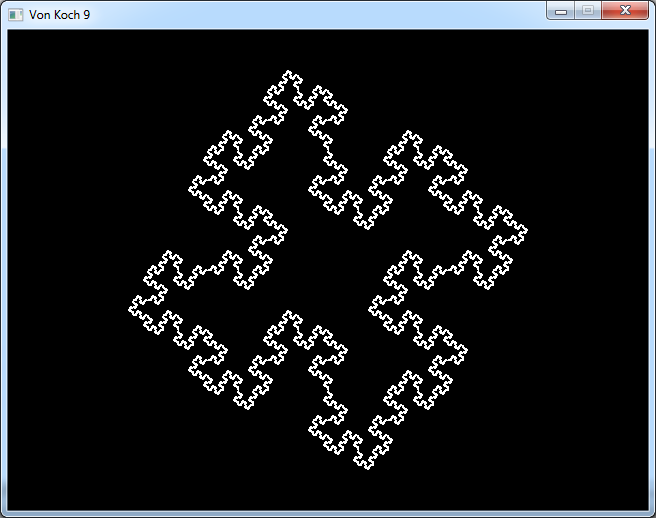
The last rule is a bit more complex:
It is inspired by the Peano curve.
Vec2f n[8];
Vec2f v12 = (p2 - p1) * 4.0f / 15.0f;
Vec2f v12b = v12;
Vec2f v12c = v12;
v12b.rotate(DEG_TO_RAD(-80));
v12c.rotate(DEG_TO_RAD(80));
n[0] = p1 + v12;
n[7] = p2 - v12;
n[1] = n[0] + v12b;
n[6] = n[7] - v12b;
n[2] = n[1] + v12;
n[5] = n[6] - v12;
n[3] = n[2] + v12c;
n[4] = n[5] - v12c;
vonKoch( p1, n[0], level + 1);
vonKoch(n[0], n[1], level + 1);
vonKoch(n[1], n[2], level + 1);
vonKoch(n[2], n[3], level + 1);
vonKoch(n[3], n[4], level + 1);
vonKoch(n[4], n[5], level + 1);
vonKoch(n[5], n[6], level + 1);
vonKoch(n[6], n[7], level + 1);
vonKoch(n[7], p2, level + 1);
Download source code
Download executable for Windows
And this is the result after 4 iterations.







 Video: Von Koch curve in Javascript
Video: Von Koch curve in Javascript Science et Vie Micro n°6
Science et Vie Micro n°6