Basic transformations

About the code

The code in this article was written using Code::Blocks and SDL 2.
You can read here a guide to install this sofware.
Although it is based on SDL, I don't use its functions directly. I have written a small library with a few basic
functions to ease the understanding and the portability to another language.
You can read more about this lib here.

This article uses the line function we added in the Bresenham's line algorithm.
And the Vec2f class we added in vectors.

Shapes

In this article I will talk about the basic 2D transformations: translation, scaling and rotation.
But to visualize them clearly we will need to draw a simple shape.
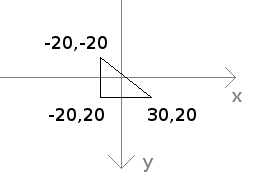
I chose a triangle centered around the origin.

As we said before, a point can be seen as a vector. So we will use the Vec2f class I introduced in the 2 last
articles.
We will see that applying a transformation to our triangle is the same as applying it to each of its points.

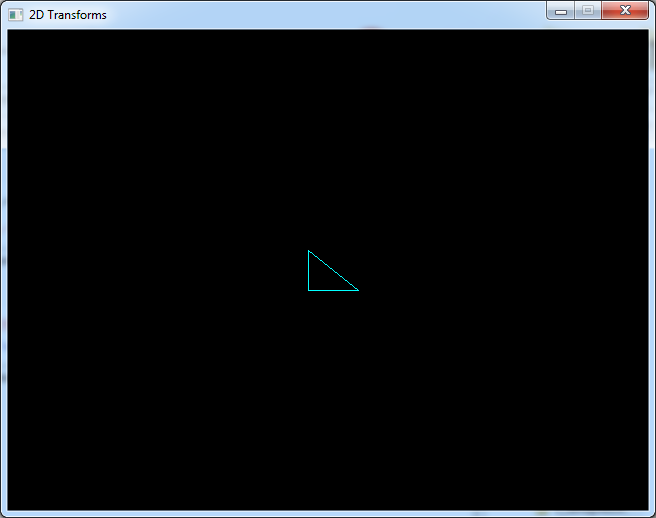
But first let's draw our triangle. In the code it is defined as an array:

		// define the shape
		Vec2f shape[] =
		{
			{-20, 20}, {-20, -20}, {30, 20}
		};

And we draw it as if the origin is at the center of the screen

		void drawShape(Vec2f* points, int nbPoints, Color color)
		{
			for (int i = 0; i < nbPoints; i++)
			{
				int next = (i + 1) % nbPoints;
				gfx.line(points[i].x + SCREEN_WIDTH  / 2,
				         points[i].y + SCREEN_HEIGHT / 2,
				         points[next].x + SCREEN_WIDTH  / 2,
				         points[next].y + SCREEN_HEIGHT / 2,
				         color);
			}
		}

		Download source code
		Download executable for Windows

And here is the result:

Translation

Translation is the easiest transformation.
We simply need to add the translation vector to each point.

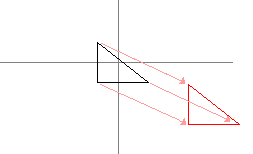
We don't need to create a special function in Vec2f, we will use the addition operator to add the vector to each
point of the shape

		void translateShape(Vec2f* points, int nbPoints, Vec2f transVector)
		{
			for (int i = 0; i < nbPoints; i++)
				points[i] += transVector;
		}

And in our main loop we will make a copy of our shape, apply the transformation, then draw it:

		while (sys.isQuitRequested() == false)
		{
			gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));

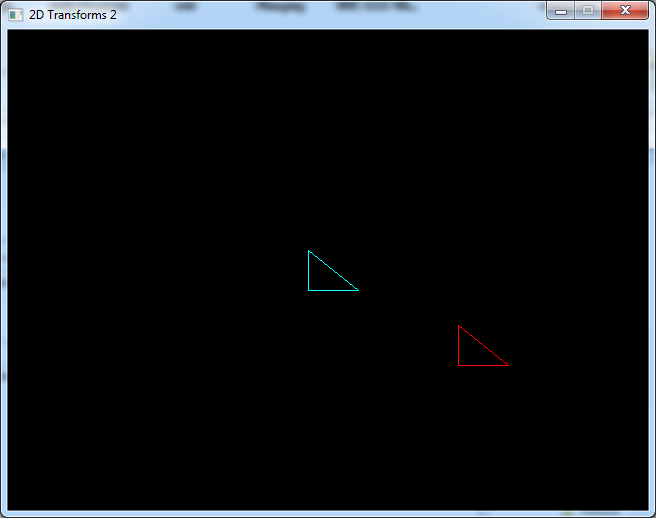
			drawShape(shape, 3, Color(0, 255, 255));

			// copy shape
			Vec2f shape2[3];

			for (int i = 0; i < 3; i++)
				shape2[i] = shape[i];

			// translate and draw
			translateShape(shape2, 3, Vec2f(150, 75));
			drawShape(shape2, 3, Color(255, 0, 0));

			gfx.render();
			sys.wait(20);
			sys.processEvents();
		}

		Download source code
		Download executable for Windows

Scaling

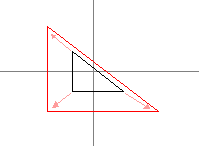
To scale our shape we need to multiply its coordinates by a float.

The Vec2f class allows us to multiply a vector by a single float. But if we want to have a different scale along x
and y we need to write a new function:

		void Vec2f::scale(const Vec2f& s)
		{
			x *= s.x;
			y *= s.y;
		}

Now if we modify our main loop to use this function on the copy of our shape

		void scaleShape(Vec2f* points, int nbPoints, Vec2f scaleVector)
		{
			for (int i = 0; i < nbPoints; i++)
				points[i].scale(scaleVector);
		}

		[...]

		while (sys.isQuitRequested() == false)
		{
			gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));

			drawShape(shape, 3, Color(0, 255, 255));

			// copy shape
			Vec2f shape2[3];

			for (int i = 0; i < 3; i++)
				shape2[i] = shape[i];

			// scale and draw
			scaleShape(shape2, 3, Vec2f(6, 3));
			drawShape(shape2, 3, Color(255, 0, 0));

		Download source code
		Download executable for Windows

We get this:

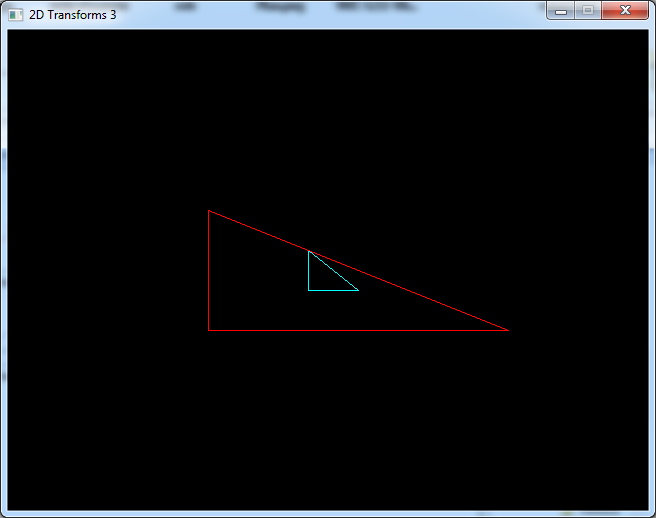
We can also use negative values to get an horizontal or vertical symetry

		// scale and draw
		scaleShape(shape2, 3, Vec2f(-6, 3));
		drawShape(shape2, 3, Color(255, 0, 0));

		Download source code
		Download executable for Windows

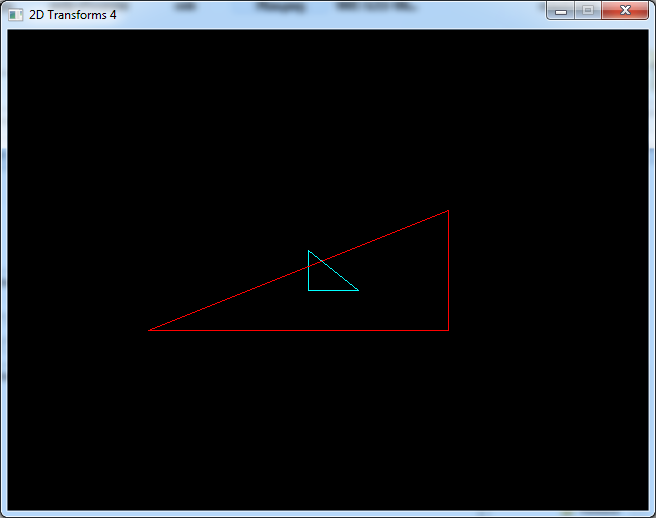
Or negative values on both axes to get a central symetry

		// scale and draw
		scaleShape(shape2, 3, Vec2f(-6, -3));
		drawShape(shape2, 3, Color(255, 0, 0));

		Download source code
		Download executable for Windows

Rotation

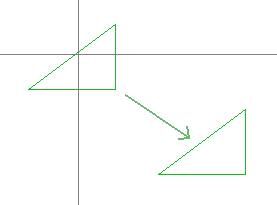
Rotation is a bit more complicated, but not so much.
In the article about circles, we already saw how to compute the image of a point that is on the horizontal axis.

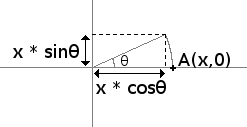
But how do we transform a point that can be anywhere on the plane ?
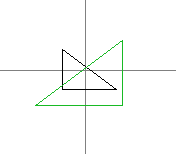
We will decompose it's coordinates to an horizontal and a vertical part:

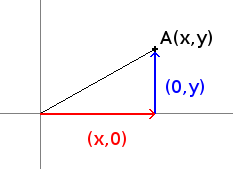
We already know how to rotate the horizontal part but what is the image of the vertical one ?

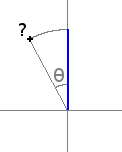
Visually, by looking at the greatest and the smallest coordinates, and correlating them with the image of the
horizontal part, we can guess the coordinates of this point:

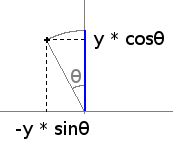
So the equations to rotate our point are:

		newX = x * cos(angle) - y * sin(angle);
		newY = x * sin(angle) + y * cos(angle);

We can add that as a new function in our Vec2f class:

		void Vec2f::rotate(const float angle)
		{
			float co = cos(angle);
			float si = sin(angle);

			float newX = x * co - y * si;
			float newY = x * si + y * co;

			x = newX;
			y = newY;
		}

Now let's test that with our shape

		void rotateShape(Vec2f* points, int nbPoints, float angle)
		{
			for (int i = 0; i < nbPoints; i++)
				points[i].rotate(angle);
		}

		[...]

		while (sys.isQuitRequested() == false)
		{
			gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));

			drawShape(shape, 3, Color(0, 255, 255));

			// copy shape
			Vec2f shape2[3];

			for (int i = 0; i < 3; i++)
				shape2[i] = shape[i];

			// rotate and draw
			rotateShape(shape2, 3, DEG_TO_RAD(30));
			drawShape(shape2, 3, Color(255, 0, 0));

		Download source code
		Download executable for Windows

And this is what we see:

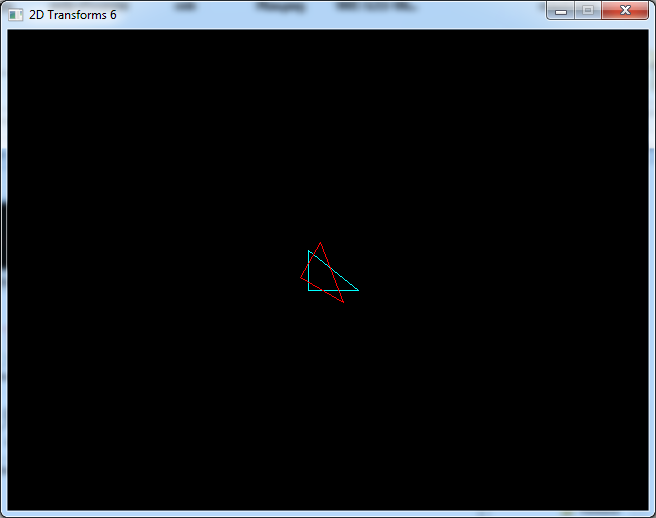
Notice that the triangle rotates in the clockwise direction because on the screen, the y coordinate increases
towards the bottom, when mathematicians usually make it increase towards the up.

Combining transformations

When you combine 2 transformations, the order you apply them is important.
For example let's combine a translation and a scaling.
In one case we will do the scale first then the translation, and in the other case we will do the opposite.

		while (sys.isQuitRequested() == false)
		{
			gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));

			drawShape(shape, 3, Color(0, 255, 255));

			// copy shape
			Vec2f shape2[3];

			for (int i = 0; i < 3; i++)
				shape2[i] = shape[i];

			// transform and draw
			scaleShape(shape2, 3, Vec2f(-2, 1));
			translateShape(shape2, 3, Vec2f(100, 50));
			drawShape(shape2, 3, Color(0, 255, 0));

			// copy shape
			Vec2f shape3[3];

			for (int i = 0; i < 3; i++)
				shape3[i] = shape[i];

			// transform and draw
			translateShape(shape3, 3, Vec2f(100, 50));
			scaleShape(shape3, 3, Vec2f(-2, 1));
			drawShape(shape3, 3, Color(255, 0, 0));

		Download source code
		Download executable for Windows

And this is what we get:

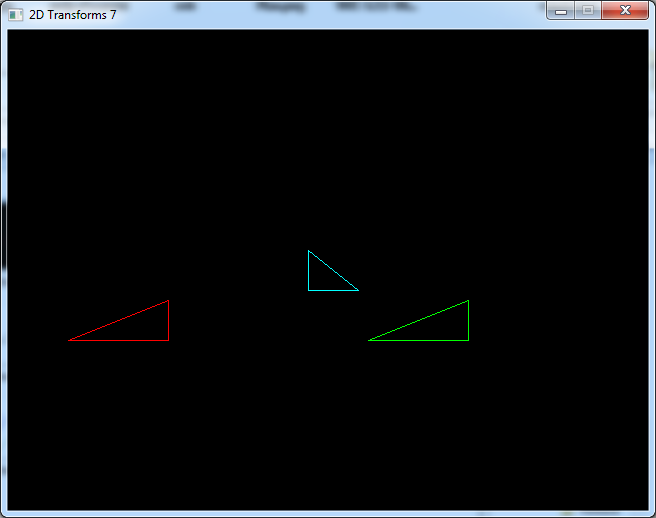
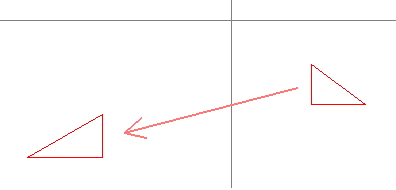
For the green triangle, we first scaled it...

...then we tranlated it:

The red one was first translated...

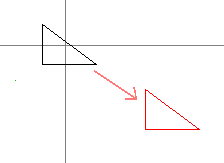
...then scaled.

If we combine a rotation and a translation we get different results too.

		float angle = 0;

		// wait until we quit
		while (sys.isQuitRequested() == false)
		{
			gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));

			drawShape(shape, 3, Color(0, 255, 255));

			// copy shape
			Vec2f shape2[3];

			for (int i = 0; i < 3; i++)
				shape2[i] = shape[i];

			// transform and draw
			rotateShape(shape2, 3, DEG_TO_RAD(angle));
			translateShape(shape2, 3, Vec2f(150, 0));
			drawShape(shape2, 3, Color(0, 255, 0));

			// copy shape
			Vec2f shape3[3];

			for (int i = 0; i < 3; i++)
				shape3[i] = shape[i];

			// transform and draw
			translateShape(shape3, 3, Vec2f(150, 0));
			rotateShape(shape3, 3, DEG_TO_RAD(angle));
			drawShape(shape3, 3, Color(255, 0, 0));

			angle += 1;

		Download source code
		Download executable for Windows

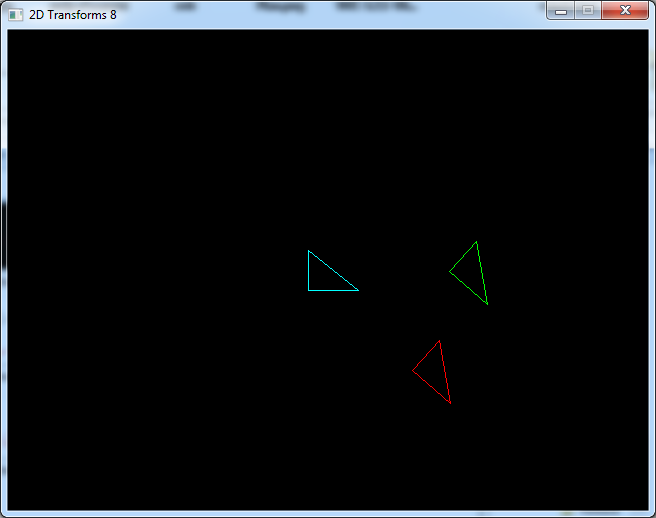
In this animated program the green triangle spins at a fixed point while the red one turns around the screen.

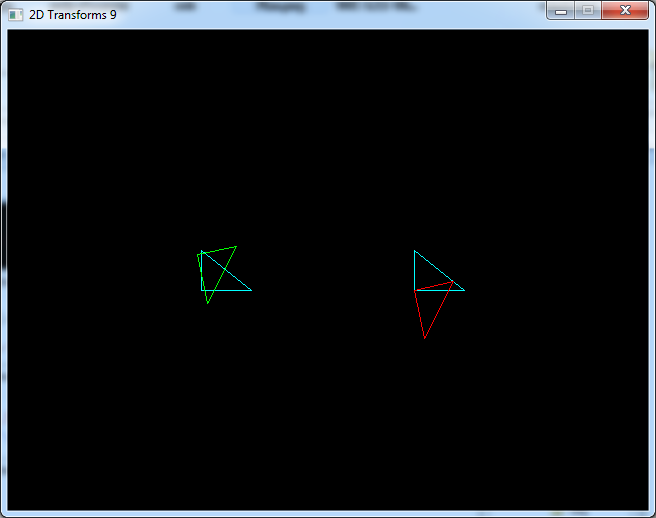
Changing the center of rotation

We can combine rotation and translations to change the center around which the shape is spinning.
A rotation is always applied around the origin of the plane. So in the case of our triangle it lies inside it as we
can see on the first image of this article.

Now suppose that we want the triangle to rotate around the right angled vertex - that is the coordinate of the
first point in the array.
We can do that by first translating the triangle so that this point gets to the origin.

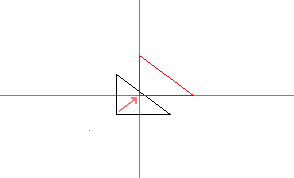
Then we rotate the triangle.

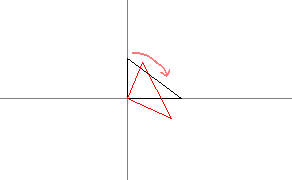
And finally we translate it back.

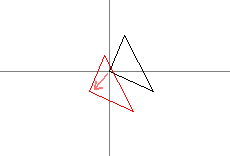
With this code you will see the diference between the 2 centers of rotation.

		void drawShapeLeft(Vec2f* points, int nbPoints, Color color)
		{
			for (int i = 0; i < nbPoints; i++)
			{
				int next = (i + 1) % nbPoints;
				gfx.line(points[i].x + SCREEN_WIDTH  / 3,
				         points[i].y + SCREEN_HEIGHT / 2,
				         points[next].x + SCREEN_WIDTH  / 3,
				         points[next].y + SCREEN_HEIGHT / 2,
				         color);
			}
		}

		void drawShapeRight(Vec2f* points, int nbPoints, Color color)
		{
			for (int i = 0; i < nbPoints; i++)
			{
				int next = (i + 1) % nbPoints;
				gfx.line(points[i].x + SCREEN_WIDTH  * 2 / 3,
				         points[i].y + SCREEN_HEIGHT / 2,
				         points[next].x + SCREEN_WIDTH  * 2 / 3,
				         points[next].y + SCREEN_HEIGHT / 2,
				         color);
			}
		}

		void translateShape(Vec2f* points, int nbPoints, Vec2f transVector)
		{
			for (int i = 0; i < nbPoints; i++)
				points[i] += transVector;
		}

		void scaleShape(Vec2f* points, int nbPoints, Vec2f scaleVector)
		{
			for (int i = 0; i < nbPoints; i++)
				points[i].scale(scaleVector);
		}

		void rotateShape(Vec2f* points, int nbPoints, float angle)
		{
			for (int i = 0; i < nbPoints; i++)
				points[i].rotate(angle);
		}

		int main(int argc, char* argv[])
		{
			// init the window
			gfx.init("2D Transforms 9", SCREEN_WIDTH, SCREEN_HEIGHT);
			gfx.init2D();

			// define the shape
			Vec2f shape[] =
			{
				{-20, 20}, {-20, -20}, {30, 20}
			};

			float angle = 0;

			// wait until we quit
			while (sys.isQuitRequested() == false)
			{
				gfx.clearScreen(Color(0, 0, 0, SDL_ALPHA_OPAQUE));

				drawShapeLeft(shape, 3, Color(0, 255, 255));
				drawShapeRight(shape, 3, Color(0, 255, 255));

				// copy shape
				Vec2f shape2[3];

				for (int i = 0; i < 3; i++)
					shape2[i] = shape[i];

				// transform and draw
				rotateShape(shape2, 3, DEG_TO_RAD(angle));
				drawShapeLeft(shape2, 3, Color(0, 255, 0));

				// copy shape
				Vec2f shape3[3];

				for (int i = 0; i < 3; i++)
					shape3[i] = shape[i];

				// transform and draw
				translateShape(shape3, 3, -shape[0]);
				rotateShape(shape3, 3, DEG_TO_RAD(angle));
				translateShape(shape3, 3, shape[0]);
				drawShapeRight(shape3, 3, Color(255, 0, 0));

				angle += 1;

				gfx.render();
				sys.wait(20);
				sys.processEvents();
			}

			gfx.quit();

			return EXIT_SUCCESS;
		}

		Download source code
		Download executable for Windows

Links

Video of the programs in this article